A
纪念一下本人在校模拟用线段树优化dp单杀*900。
最小和最大没有本质区别,这里只讨论最小的情况。
设 \(f_i\) 表示前缀 \(i\) 的答案,显然是要枚举 \(j\) 使得 \((j, i]\) 合并成一段:
其中 \(s_i = \sum_{i = 1}^i a_i\)。
想办法把 \(i, j\) 的贡献拆开,再用数据结构优化转移。
显然有 $ \lceil \dfrac{s_i - s_j}{x} \rceil = \lfloor \dfrac{s_i - s_j}{x} \rfloor + [s_i \not\equiv s_j \pmod x]$,对于下取整,我们有广为人知的结论:
证明也很简单,对于三种不等关系讨论一下即可。
两者结合一下:
把所有 \(s_i \bmod x\) 离散化,用线段树优化转移即可。submission
B
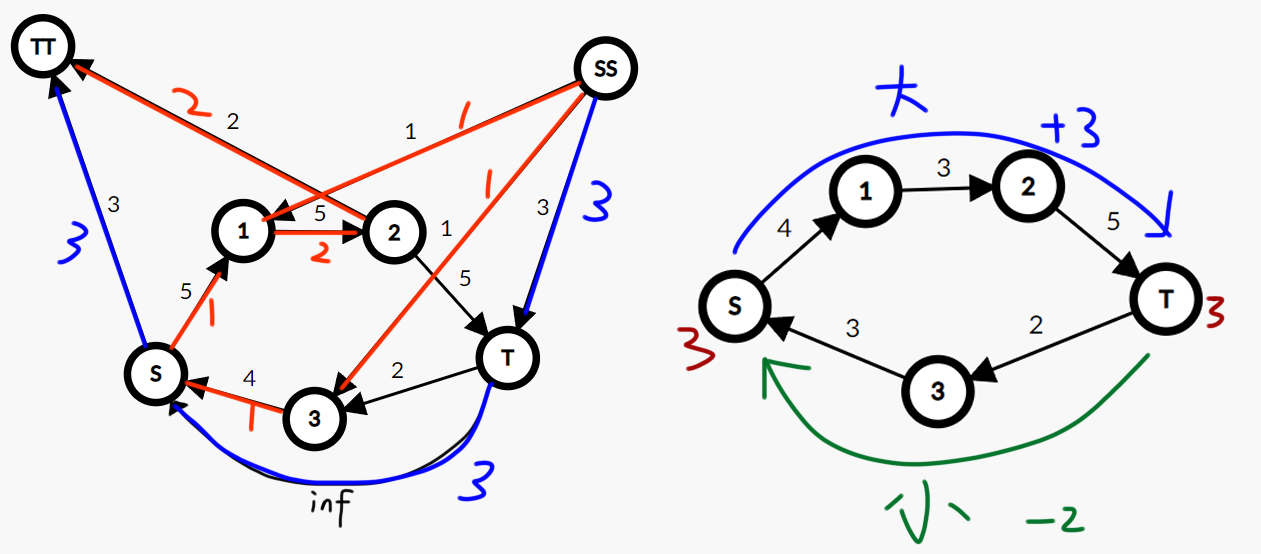
存在平凡的构造使得权值为零:\(1\) 向其他点连 \(d_i\) 的边,任意 \(i > 1\) 向 \(1\) 连 \(-d_i\) 的边。
几条显而易见的性质:
- \(i\) 不能向 \(d_j \ge d_i\) 的 \(j\) 连负权边,否则 \(d_i + w < d_j\),不满足最短路的限制。
- \(i\) 最多向 \(d_j < d_i\) 的 \(j\) 连权值为 \(d_j - d_i\) 的边,否则出现负环(不满足最短路限制)。
因此,我们得到了答案的下界:
那么是否存在一组构造能达到下界呢?
将 \(d\) 排序,\(i\) 向 \(i + 1\) 连 \(d_{i + 1} - d_i\) 的边,所构成的一条链显然满足初始限制。
每个 \(i\) 对于 \(j < i\) 连 \(d_j - d_i\) 的边,一定不会出现负环,且始终满足最短路的限制,这样就达到了下界。
submission
C
把第一次染色的颜色作为根,枚举根,对每种情况分别求一下答案,最后除以 \(n\)(第一步是等概率的)。
考虑 \(u > v\) 对整棵树的贡献 \(e(u, v) = p(u, v) \times 1 = p(u, v)\),设 \(l = \text{lca}(u, v)\)。
当 \(l\) 未被染色时,局面可以是任意的;当 \(u, v\) 都已经染色后,局面也可以是任意的。
全局的概率是 \(1\),不对 \(p(u, v)\) 产生影响,只要考虑 \(l\) 被染色到 \(v\) 被染色之间的这一过程。
我们称 \((u, v)\) 简单路径上的点是关键的。
一旦 \(l\) 被染色,每次操作染色集合有 \(p\) 的概率向 \(u\) 逼近一步,\(p\) 的概率向 \(v\) 逼近,\(1 - 2p\) 的概率选择非关键点。
注意每次操作的 \(p\) 可能不同,但向 \(u, v\) 逼近的概率始终相同(等概率)。
设 \(f(i, j)\) 表示 \(l\) 要向 \(u\) 逼近 \(i\) 步,向 \(v\) 逼近 \(j\) 步,最后 \(u\) 出现在 \(v\) 之前的概率。
\(f(i, j) = p\times f(i, j - 1) + p \times f(i - 1, j) + (1 - 2p) \times f(i, j) \implies f(i, j) = \frac{f(i - 1, j) + f(i, j - 1)}{2}\)。submission