四元数

news/2024/10/3 2:26:56

四元数

定义

【四元数的可视化】 https://www.bilibili.com/video/BV1SW411y7W1/?share_source=copy_web&vd_source=ac806c24de13bf5f509bf105a8578e24

\[0.00 + 8.46i + 2.64j + 3.38k\\ \]

最左侧实数称为标量部分，右侧\(ijk\)虚部称为向量vector

\[i^2+j^2+k^2=1\\ ij=-ji=k\\ ki=-ik=j\\ jk=-kj=i \]

\[(w_1 + x_1i + y_1j + z_1k)(w_2 + x_2i + y_2j + z_2k)\\ =(w_1w_2 - x_1x_2 - y_1y_2 - z_1z_2)\\ +(w_1x_2 + x_1w_2 + y_1z_2 - z_1y_2)i\\ +(w_1y_2 + y_1w_2 + z_1x_2 - x_1z_2)j\\ +(w_1z_2 + z_1w_2 + x_1y_2 - y_1x_2)k \]

用四元数来描述矩阵相乘

\[\vec v_1=\begin{bmatrix}x_1\\y_1\\z_1\end{bmatrix} =(w_1 + x_1i + y_1j + z_1k)\\ q_1=(w_1,\ \vec v_1) \\ \vec v_2=\begin{bmatrix}x_x\\y_x\\z_x\end{bmatrix} =(w_2 + x_2i + y_2j + z_2k)\\ q_2=(w_2,\ \vec v_2) \\ q_1\cdot q_2=(w_1w_2 - \vec v_1\cdot \vec v_2,\ w_1\vec v_2 + w_2\vec v_1 + \vec v_1 \times \vec v_2) \]

\(q_1\cdot q_2 = (\frac{q_1}{\lVert q_1\rVert})\lVert q_1 \rVert\cdot q_2\)

\(q_1\cdot q_2\)会将\(q_2\)的大小拉伸到\(q_1\)的大小（上市括号外的内容），然后施加一个特殊的四维旋转（上式括号内的内容）

四维超球投影到三维空间，在单位球内的是\([-1,1]^4\)，超出\([-1,1]^4\)的点投影到了单位球外，延申至无穷远

投影过程可参考二维到一维、三维到二维的球极投影

四元数在三维点上的应用

【四元数和三维转动，可互动的探索式视频（请看链接）】 https://www.bilibili.com/video/BV1Lt411U7og/?share_source=copy_web&vd_source=ac806c24de13bf5f509bf105a8578e24

当想绕某个轴旋转某个角度时，首先用一个单位向量（\(ijk\)经过归一化，三者平方和为\(1\)）定义这个轴，对于三维向量，其实部为\(0\)，\(xyz\)作为\(ijk\)的系数

之后，若想旋转的角度是\(\theta\)，则使用半角\(\theta/2\)的余弦值作为实部，正弦值乘以四元数向量

如:\(q=(\cos(40^{\circ}/2)+\sin(40^{\circ}/2)(0.67i-0.67j-0.33k))\)

如果想对一点\(p\)应用这个旋转，只需\(p'=q\cdot p\cdot q^{-1}\)即可，就能得到旋转后的坐标\(p'\)，\(p'\)是一个四元数，其实部为0，\(ijk\)向量系数即为旋转后的三维坐标

为什么是\(q\cdotp\cdot q^{-1}而不是q\cdot p\)？

\(q\)的本质是一个空间变换，旋转变换是其中一环，旋转*缩放=空间变换

四元数有一个性质是可逆的

那么(旋转*缩放)p / 缩放 = 旋转*p？

然而这样做是不行的，因为空间变换\(q\)必定包含旋转和缩放

于是可以用到左右手螺旋定则

\(q\)左乘\(p\)或右乘\(p\)，只会影响旋转的方向，不会影响缩放的方向

而\(q\cdot p\)和\(q^{-1}\cdot p\)的异同在于二者旋转一样缩放相反

于是可以通过\(q\cdot p\cdot q^{-1}\)，左乘\(q\)和右乘\(q^{-1}\)分别完成半个\(\theta\)角度的旋转，而\(q\)与\(q^{-1}\)又刚好抵消掉了缩放

四元数插值

要在两个四元数之间进行球面线性插值(Spherical Linear Interpolation), Slerp()。球面线性插值可在球面表面大圆的弧线上做匀速率运动，因此对于旋转插值有两个期望的性质

旋转插值路径使得扭矩最小化：两个旋转之间的路径是旋转空间中所能得到的最短路径
插值有很顶角速度：动画参数\(t\)的变化量和所得旋转的变换了的关系在插值过程中是恒定的，换句话说，在插值范围内，插值速度是恒定的

\[slerp(q_1, q_2. t)=\frac{q_1\sin((1-t)\theta)+q_2\sin(t\theta)}{\sin\theta}\\ t\in[0,1] \]

Shoemake(1985)提出的公式

\[q_\bot=q_2-(q_1\cdot q_2)q_1 \\ q'=q_1\cos(\theta t)+\hat q_\bot\sin(\theta t) \]

PBRT中的公式

以一种更直观的方式理解

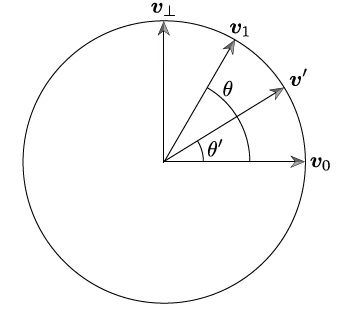
考虑在2D平面下的两个单位圆上的向量\(v_0\)和\(v_1\)，二者夹角为\(\theta\)，想要计算二者之间角度为\(\theta'\)的插值向量，可以寻找正交于\(v_0\)的向量\(v_\bot\)，再应用三角恒等式\(v'=v_0\cos\theta'+v_\bot\sin\theta'\)

那么要计算\(q'\)，首先要在四元数空间种计算一个正交坐标系，一个轴为\(q_1\)，另一个是于\(q_1\)正交的四元数\(q_\bot\)，这样两轴就构成张开\(q_1\)和\(q_2\)的基

可以通过将\(q_2\)投影到\(q_1\)，再由\(q_2\)减去这一部分得到\(q_\bot\)

\(q_\bot=q_2-(q_1\cdot q_2)q_1\)

那么插值四元数为\(q'=q_1\cos(\theta t)+\hat q_\bot\sin(\theta t)\)