题面

$\quad $ 我们记 \(F(x)\) 为 \(x\) 为真的方案数,\(len\) 为序列最长连续相同子段长度。
$\quad $ 那么就有:
$\quad $ 也就是:
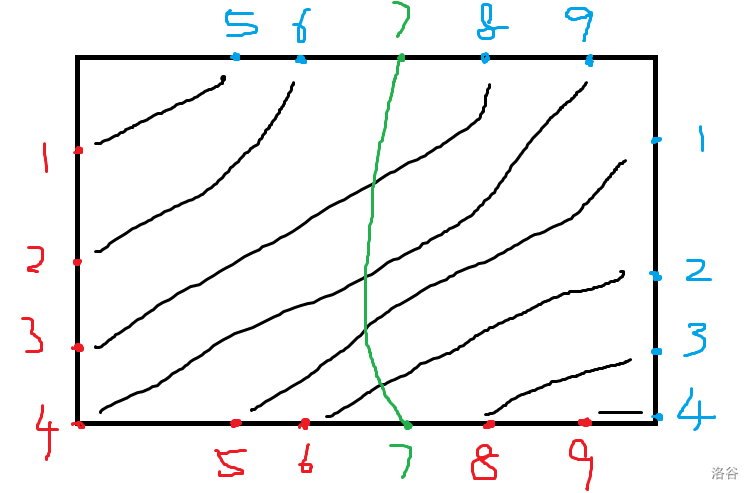
$\quad $ 这里可以画个图,发现结果形如三角形,即可得出上式。再改变一下形式:
$\quad $ 然后考虑如何求解 \(F(len<=i)\) ,我们枚举这个序列分为 \(j\) 个区间,这些区间中元素的颜色一致且相邻区间颜色不同。可以发现,这样覆盖了全部的情况。
$\quad $ 发现所有区间的长度都小于等于 \(i\) 比较难做,没有限制的直接插空即可解决,所以我们考虑容斥,枚举这 \(j\) 个区间里有 \(k\) 个是长度大于 \(i\) 的,然后对于每一个枚举出来的 \(k\) ,我们将这几个区间长度减去 \(i\) ,那么这个问题就可以拿插空做了。于是得出式子:
$\quad $ 我们更换枚举顺序:
\begin{aligned}
ans&=nm ^{n} -\sum _{i=1}^{n-1}\sum _{k=0}^{n}(-1) ^{k}m\sum _{j=k}^{n}(m-1) ^{j-1}C _{j}^{k} C _{n-ik-1}^{j-1}\\
&=nm ^{n} -\sum _{i=1}^{n-1}\sum _{k=0}^{n}(-1) ^{k}m(n-ik) ^{-1}\sum _{j=k}^{n}(m-1) ^{j-1}C _{j}^{k} C _{n-ik}^{j}j
\end{aligned}
$\quad $ 现在看最后那个和式的组合意义。
$\quad $ 我们在 \(n-ik\) 个数中先选出 \(j\) 个数,再在这 \(j\) 个数中选出 \(k\) 个数,然后在 \(j\) 中选出一个数(下文记作 \(x\) )不染色,并对剩下的 \(j-1\) 个数染色,(这里的染色就是确定每个元素的种类,并且每个数只有 \(m-1\) 种可能)。
$\quad $ 然后我们可以先选出这 \(k\) 个数,然后再选出 \(x\)(注意 \(x\) 可以在那 \(k\) 个数中),然后去找能够包含他们的、大小为 \(j\) 的集合,并对集合中剩下的元素染色。
$\quad $ 对于现已经选择的数之外的数,他可以是选或不选,如果选了就有 \(m-1\) 种可能,那么就可以直接看做是给这些数染色,不过这里的每个元素有 \(m\) 种可能。
$\quad $ 那么这个时候 \(x\) 的位置就很重要了,这里就分出两种情况, \(x\) 在选出的 \(k\) 个数里、\(x\) 不在那 \(k\) 个数里。
$\quad $ 当 \(x\) 在那 \(k\) 个数中时,答案就是 \(C _{k}^{1}(m-1) ^{k-1}m ^{n-ik}\) ,也就是先确定出 \(x\) 的可能,然后对剩下的 \(k-1\) 个元素染色,再对这 \(k\) 个数外的的元素染色。注意这两种元素的染色可能数并不相同,见上文。
$\quad $ 当 \(x\) 不在那 \(k\) 个数里时,答案就是 \(C _{n-ik}^{1}(m-1) ^{n-ik-1} m ^{k}\) 。原理和上一种情况一样。
$\quad $ 那么我们就得出了最终的答案:
后记
$\quad $ 开始推式子的时候看 \(C _{j}^{k} C _{n-ik}^{j}\) 不是很顺眼,然后就给它展开凑项变成了 \(C _{n-ik}^{k}C _{n-ik-k}^{j-k}\) ,然后发现这个东西是可以推广的,也就是:
$\quad $ 证明:
$\quad $ 然后以为自己发现了什么了不得的东西,但是一想自己没那么厉害,怎么可能发现了前人没发现的东西,搜了一下发现在《具体数学》里提及了。