AGC061F 做题记录

link

事实上这是 CSP模拟赛 #36 的 T4。

记 \(a_i,b_i\) 分别为前 \(i\) 个字符中 \(0\) 的个数对 \(n\) 取模后的值，\(1\) 的个数对 \(m\) 取模后的值。那么，记 \(k\) 为序列长度，合法的序列满足：

• \(\forall 1\le i < j\le k ,\ (a_i, b_i) \not = (a_j, b_j)\)

• \(a_k = b_k = 0\)

相当于一张循环网格，从 \((0, 0)\) 开始走，每次向上或向右走一格，中途不能经过重复的格子，最终回到 \((0, 0)\) 的方案数。

考虑断环为链，拎出所有碰到上 / 右边界回到下 / 左边界的位置，例如下图：

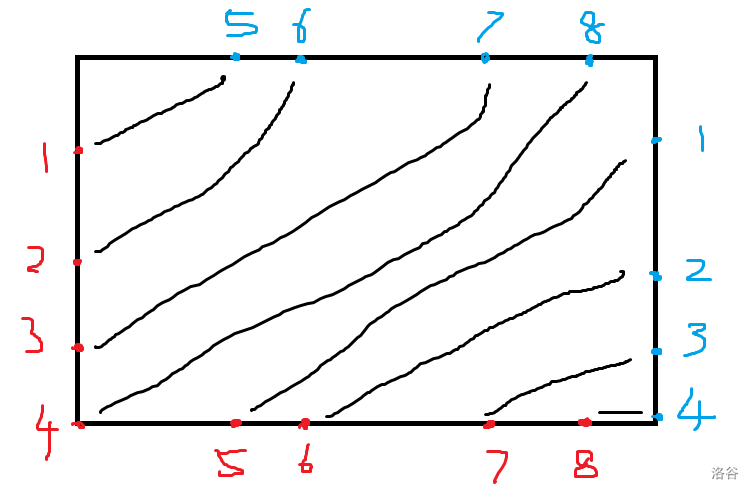
其中蓝点为上 / 右边界的点，红点为下 / 左边界的点，令红点的坐标分别为 \((-1, 0\dots m - 1), (0\dots n - 1, -1)\)，蓝点同理，可以发现:

• 相同编号的每个蓝点与对应红点坐标的另一维相同。

• \((0, -1)\) 和 \((-1, 0)\) 两个位置恰好存在一个红点，蓝点类似。

• 按从左到右，从上到下的顺序依次匹配所有红点和蓝点（如 \(1-5, 2 - 6\) 等）。

• 设左边界有 \(r\) 个红点，下边界有 \(c\) 个红点，整条路径形成一个环的充要条件是 \(\gcd(r, c) = 1\)。

对于第二点，我们可以钦定 \((-1, 0)\) 有红点，然后交换 \(n\) 和 \(m\) 再做一遍。

由于每个格子至多经过一次，可以使用 LGV 引理解决问题。由于算出的答案是带符号的，最终需要乘上 \((-1) ^{rc}\)。

考虑如何对所有红蓝点的情况统计答案。由于红蓝点总是成对出现的，可以视为从所有红蓝点中删掉若干对。例如红点 \((-1, 3)\) 和蓝点 \((n, 3)\)，我们可以在两点之间额外连一条边表示删掉这两个点。

观察这样做是否正确。对于一对固定 \((r, c)\)，符号 \((-1) ^{rc}\) 不会改变：

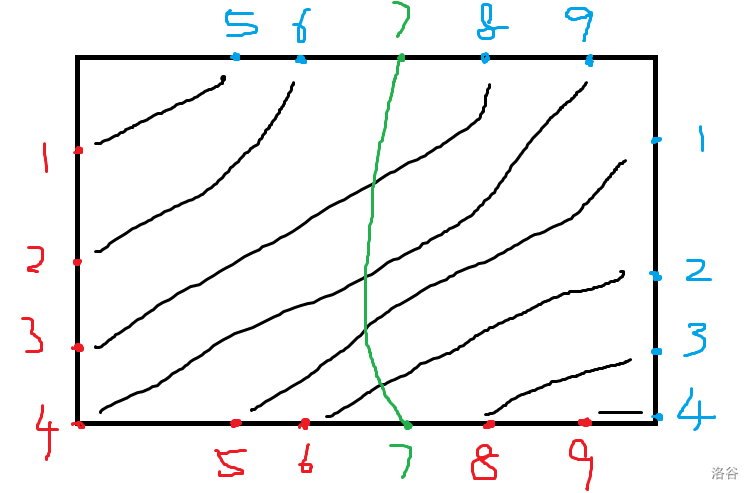
如图，不加入 \(7\) 时的匹配排列为 \((5,6,8,9,1,2,3,4)\)，加入 \(7\) 后排列为 \((5,6,8,9,1,2,7,3,4)\)，其贡献的逆序对数量恰好是下边界中的 \(5\) 和 \(6\) 号红点，以及右边界的 \(1\) 和 \(2\) 号红点。可以看出，\(1,2\) 号红点恰好匹配 \(5,6\) 号蓝点，所以贡献被抵消了。

因此我们只需要知道最终方案的 \(r,c\) 即可快速计算答案，可以加入两个元 \(x,y\) 来占位。我们令左边界的红点直接连向对应蓝点的边权为 \(x\)，下边界的则为 \(y\)。在矩阵中 \(a_{i, j}\) 值是可能带有 \(x, y\) 的。通过计算矩阵行列式，得到最终的二元生成函数 \(F(x, y)\)，最后答案即为 \(\sum\limits_{r = 0} ^ {n} \sum\limits_{c = 0} ^ m [\gcd(r, c) = 1]\cdot [x^{n - r}y^{m - c}]F(x, y)\cdot (-1) ^{rc}\)。

行列式不好直接计算，可以拉格朗日插值直接算出多项式。需要带入 \(\mathcal O(nm)\) 个点值，计算行列式需要 \(\mathcal O((n + m) ^ 3)\) 的时间，总时间复杂度为 \(\mathcal O(nm(n + m) ^ 3)\)。

• 启示：断环为链思想；等价模型转化，且不影响答案计算方式。

点击查看代码

#include <bits/stdc++.h>
#define ll long long
#define ull unsigned ll
#define fi first
#define se second
#define pir pair <ll, ll>
#define mkp make_pair
#define pb push_back
using namespace std;
void rd(ll &x) {char c; ll f = 1;while(!isdigit(c = getchar()))if(c == '-') f = -1;x = c - '0';while(isdigit(c = getchar())) x = x * 10 + c - '0';x *= f;
}
const ll maxn = 85, mod = 998244353;
ll n, m, a[maxn][maxn], C[maxn][maxn], lim;
ll pls(const ll x, const ll y) { return x + y >= mod? x + y - mod : x + y; }
void add(ll &x, const ll y) { x = x + y >= mod? x + y - mod : x + y; }
ll power(ll a, ll b = mod - 2) {ll s = 1;while(b) {if(b & 1) s = s * a %mod;a = a * a %mod, b >>= 1;} return s;
}
struct Poly {ll dat[44];Poly() { memset(dat, 0, sizeof dat); }ll operator[] (ll x) const { return dat[x]; }ll &operator[] (ll x) { return dat[x]; }
} f[44]; ll _[44];
Poly operator + (const Poly A, const Poly B) {Poly ret;for(ll i = 0; i <= lim; i++) ret[i] = pls(A[i], B[i]);return ret;
}
Poly operator - (const Poly A, const Poly B) {Poly ret;for(ll i = 0; i <= lim; i++) ret[i] = pls(A[i], mod - B[i]);return ret;
}
Poly operator * (const Poly A, const ll k) {Poly ret;for(ll i = 0; i <= lim; i++) ret[i] = k * A[i] %mod;return ret;
}
Poly g[44], cc;
ll det() {ll prod = 1;for(ll i = 0; i < n + m; i++) {if(!a[i][i]) {prod = mod - prod;for(ll j = i + 1; j < n + m; j++)if(a[j][i]) { swap(a[i], a[j]); break; }} ll inv = power(a[i][i]);for(ll j = i + 1; j < n + m; j++) {ll tmp = mod - a[j][i] * inv %mod;for(ll k = i; k < n + m; k++)add(a[j][k], a[i][k] * tmp %mod);}}for(ll i = 0; i < n + m; i++) prod = prod * a[i][i] %mod;return prod;
}
ll w[44], tmp[44];
ll solve(ll n, ll m) {memset(f, 0, sizeof f);memset(g, 0, sizeof g);memset(tmp, 0, sizeof tmp), tmp[0] = 1;for(ll i = 1; i <= m + 1; i++)for(ll j = i - 1; ~j; j--) {add(tmp[j + 1], tmp[j]);tmp[j] = tmp[j] * (mod - i) %mod;}for(ll x = 1; x <= n + 1; x++) {for(ll y = 1; y <= m + 1; y++) {memset(a, 0, sizeof a);for(ll i = 0; i < n + m; i++)for(ll j = 0; j < n + m; j++) {ll p = j < n? j : n - 1,q = j < n? m - 1 : j - n;if(i < n) p -= i;else q -= i - n;if(p >= 0 && q >= 0)a[i][j] = C[p + q][p];}for(ll i = 1; i < n + m; i++)add(a[i][i], i < n? x : y);w[y] = det();}for(ll j = 1; j <= m + 1; j++) {memcpy(_, tmp, sizeof tmp);ll Inv = power(mod - j);for(ll i = 0; i <= m; i++) {_[i] = _[i] * Inv %mod;add(_[i + 1], mod - _[i]);}ll prod = 1;for(ll k = 1; k <= m + 1; k++)if(j ^ k) prod = prod * (j + mod - k) %mod;prod = power(prod) * w[j] %mod;for(ll i = 0; i <= m; i++)add(f[x][i], _[i] * prod %mod);}} memset(tmp, 0, sizeof tmp), tmp[0] = 1;for(ll i = 1; i <= n + 1; i++)for(ll j = i - 1; ~j; j--) {add(tmp[j + 1], tmp[j]);tmp[j] = tmp[j] * (mod - i) %mod;}for(ll i = 1; i <= n + 1; i++) {memcpy(_, tmp, sizeof tmp);ll Inv = power(mod - i);for(ll j = 0; j <= n; j++) {_[j] = _[j] * Inv %mod;add(_[j + 1], mod - _[j]);}ll prod = 1;for(ll j = 1; j <= n + 1; j++)if(i ^ j) prod = prod * (i + mod - j) %mod;prod = power(prod);cc = f[i] * prod;for(ll j = 0; j <= n; j++)g[j] = g[j] + cc * _[j];}ll ans = 0;for(ll i = 0; i <= n; i++)for(ll j = 0; j <= m; j++) {if(__gcd(n - i, m - j) == 1)add(ans, (((n - i) * (m - j)) & 1? mod - 1 : 1)* g[i][j] %mod);} return ans;
}
int main() {scanf("%lld%lld", &n, &m); lim = max(n, m);C[0][0] = 1;for(ll i = 1; i <= n + m; i++) {C[i][0] = 1;for(ll j = 1; j <= i; j++)C[i][j] = pls(C[i - 1][j], C[i - 1][j - 1]);}printf("%lld", pls(solve(n, m), solve(m, n)));return 0;
}