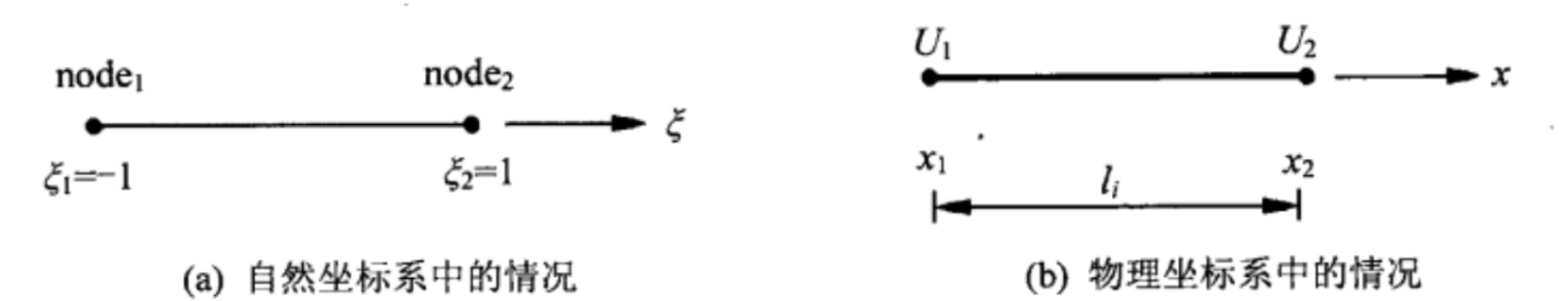在自然坐标系中 , \(\xi_2=1\)和 \(\xi_2=1\),在物理坐标系中为 \(x_1\) 和\(x_2\),相应的节点位移为\(u_1\) 和\(u_2\) 。
在自然坐标系 下,单元形函数为
\[N_{1}(\xi)=\frac{1}{2}(1-\xi)\\N_{2}(\xi)=\frac{1}{2}(1+\xi)
\]
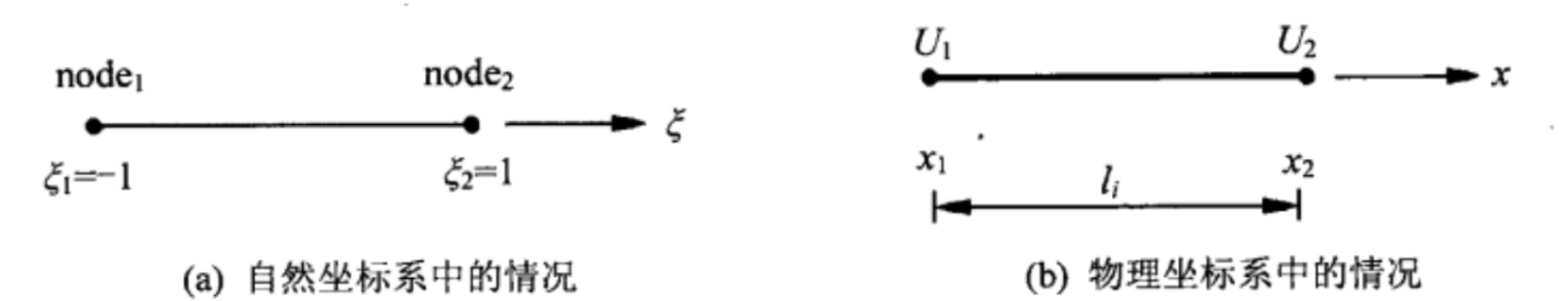
利用形函数,在自然坐标系下单元内的任一点 \(-1<\xi<1\)可以映射到物理物理坐标系下
\[x=N_{1}(\xi)x_{1}+N_{2}(\xi)x_{2}
\]
用同样的形函数对单元的位移变量进行差值
\[u=N_1(\xi)u_1+N_2(\xi)u_2
\]
这种采用相同的形函数进行坐标变换和节点变量插值,并且用相同节点数的单元称为等参单元,这种变换称为等参变换.如果变换用的节点数大于函数插值用的节点数,则称为超参变换;反之,如果变换用的节点数小于函数插值用的节点数,则称为次参变换,
为了便于在规格化的自然坐标系下进行单元特性矩阵的计算,需要建立两个坐标系间导数、面积微元、体积微元的变换关系。
对于一维单元
\[\frac{\mathrm{d}u}{\mathrm{d}x}=\frac{\mathrm{d}N_{1}(\xi)}{\mathrm{d}x}u_{1}+\frac{\mathrm{d}N_{2}(\xi)}{\mathrm{d}x}u_{2}=\frac{\mathrm{d}N_{1}(\xi)}{\mathrm{d}\xi}\frac{\mathrm{d}\xi}{\mathrm{d}x}u_{1}+\frac{\mathrm{d}N_{2}(\xi)}{\mathrm{d}\xi}\frac{\mathrm{d}\xi}{\mathrm{d}x}u_{2}
\]
由\(x=N_{1}(\xi)x_{1}+N_{2}(\xi)x_{2}\)
\[\frac{\mathrm{d}x}{\mathrm{d}\xi}=\frac{\mathrm{d}N_{1}(\xi)}{\mathrm{d}\xi}x_{1}+\frac{\mathrm{d}N_{2}(\xi)}{\mathrm{d}\xi}x_{2}=\frac{1}{2}(x_{2}-x_{1})=\frac{1}{2}l_{i}
\]
式中 \(l_i=x_2-x_2\) 是单元的长度
式\(\frac{\mathrm{d}x}{\mathrm{d}\xi}\)称为jabobi值,可以表示为 \(J=\frac{\mathrm{d}x}{\mathrm{d}\xi}\),将其代入\(\frac{\mathrm{d}u}{\mathrm{d}x}\),得
单元形函数
下面列举了部门单元形函数,更多的形函数参考 有限元法原理与应用 (朱伯芳)
八节点的四边形等参单元
\[\begin{aligned}
&N_{1}= \frac{1}{4}(1-\xi)(1-\eta)(-1-\xi-\eta) \\
&N_{2}= \frac{1}{4}(1+\xi)(1-\eta)(-1+\xi-\eta) \\
&N_{3}= \frac{1}{4}(1+\xi)(1+\eta)(-1+\xi+\eta) \\
&N_{4}= \frac{1}{4}(1-\xi)(1+\eta)(-1-\xi+\eta) \\
&N_{s}= \frac{1}{2}(1-\xi^{2})(1-\eta) \\
&N_{6}= \frac12(1+\xi)(1-\eta^2) \\
&N_{7}= \frac{1}{2}(1-\xi^{2})(1+\eta) \\
&N_{8}= \frac{1}{2}(1-\xi)(1-\eta^{2})
\end{aligned}
\]
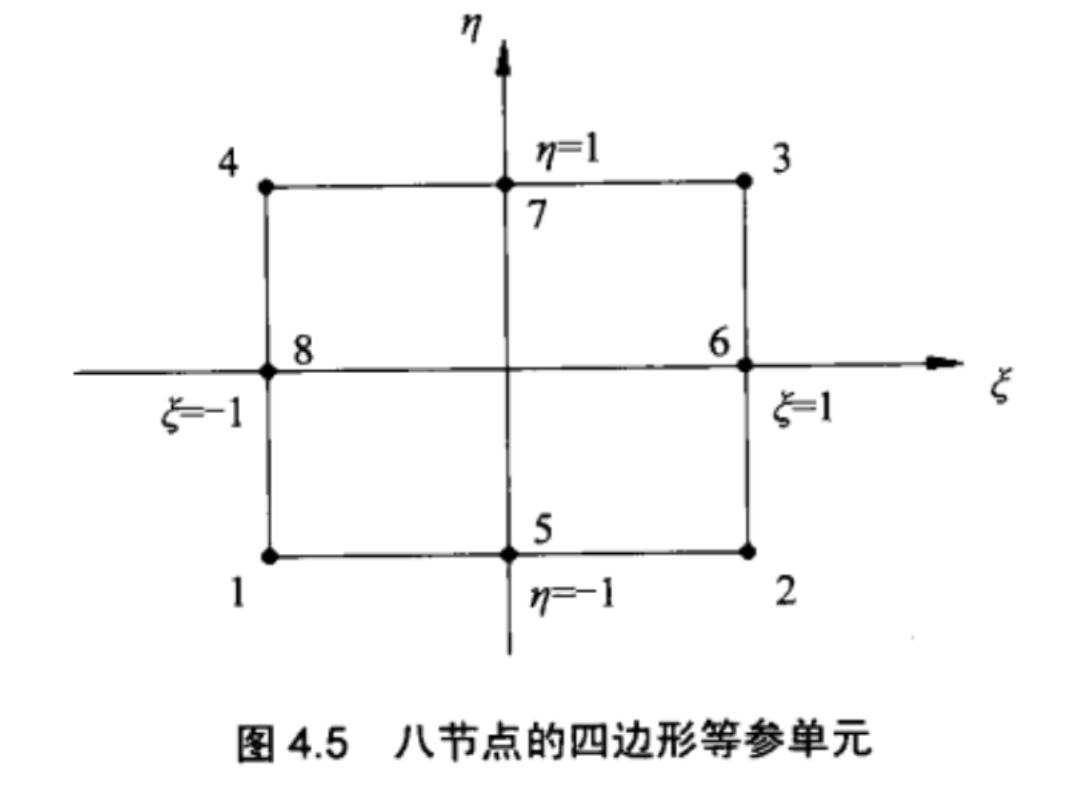
九节点的四边形等参单元
\[\begin{aligned}&\\&N_{1}=\frac{1}{2}(\xi^{2}-\xi)(\eta^{2}-\eta)\\&N_{2}=\frac{1}{2}(\xi^{2}+\xi)(\eta^{2}-\eta)\\&N_{3}=\frac{1}{2}(\xi^{2}+\xi)(\eta^{2}+\eta)\\&N_{4}=\frac{1}{2}(\xi^{2}-\xi)(\eta^{2}+\eta)\\&N_{3}=\frac{1}{2}(1-\xi^{2})(\eta^{2}-\eta)\\&N_{6}=\frac{1}{2}(\xi^{2}+\xi)(1-\eta^{2})\\&N_{7}=\frac{1}{2}(1-\xi^{2})(\eta^{2}+\eta)\\&N_{8}=\frac{1}{2}(\xi^{2}-\xi)(1-\eta^{2})\\&N_{9}=\frac{1}{2}(1-\xi^{2})(1-\eta^{2})\end{aligned}
\]
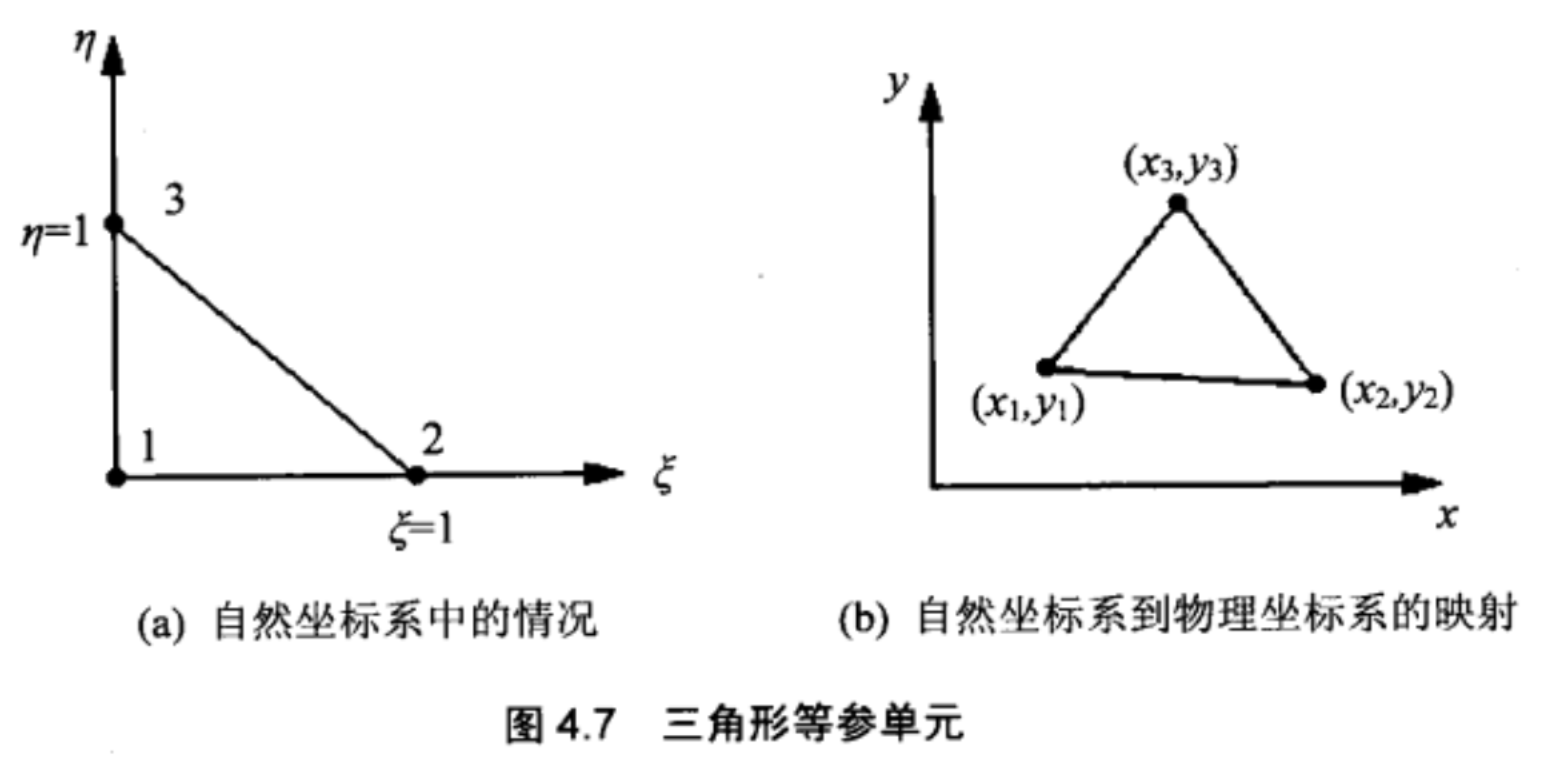
线性三角形形函数
\[\begin{aligned}&N_{1}=1-\xi-\eta\\&N_{2}=\xi\\&N_{3}=\eta\end{aligned}
\]
六节点三角形单元的形函数
\[\begin{aligned}
&N_{1}=(1-\xi-\eta)(1-2\xi-2\eta) \\
&N_{2}=\xi(2\xi-1) \\
&N_{3}=\eta(2\eta-1) \\
&N_{4}=4\xi(1-\xi-\eta) \\
&N_{5}=4\xi\eta \\
&N_{6}=4\eta(1-\xi-\eta)
\end{aligned}
\]
八节点正六面体单元
\[N_{1}=\frac{1}{8}(1-\xi)(1-\eta)(1-\zeta)\\
N_{2}=\frac{1}{8}(1+\xi)(1-\eta)(1-\zeta)\\
N_{3}=\frac{1}{8}(1+\xi)(1-\eta)(1+\zeta)\\
N_{4}= \frac{1}{8}(1-\xi)(1-\eta)(1+\zeta) \\
N_{5}= \frac{1}{8}(1-\xi)(1+\eta)(1-\zeta) \\
N_{6}= \frac{1}{8}(1+\xi)(1+\eta)(1-\zeta) \\
N_{7} =\frac{1}{8}(1+\xi)(1+\eta)(1+\zeta) \\
N_{8} =\frac{1}{8}(1-\xi)(1+\eta)(1+\zeta)
\]
参考文献
Matlab有限元结构动力学分析与工程应用-徐斌
有限元法原理与应用 (朱伯芳)