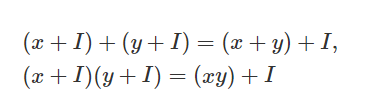1. 主成分分析 PCA
PCA:寻找最能够 表示 原始数据的投
影方法,对数据进行降维,除去冗余的信息。——不考虑类别
1.1 PCA 主要步骤
-
计算 散布矩阵 \(S\)(或者样本的协方差矩阵)
\[S = \sum_{i=1}^{n}(\bm{x}_i - \bm{\mu})(\bm{x}_i - \bm{\mu})^{\text{T}} \]其中 \(\bm{\mu} = \frac{1}{n}\sum_{i=1}^{n} \bm{x}_i\) 。
-
由 \(S\bm{e}_i = \lambda_i \bm{e}_i\) 计算 \(S\) 的 特征值 \(\lambda_i\) 和 特征向量 \(\bm{e}_i\)。\(\bm{e}_i\) 也称为主成分,任意两个主成分 正交,且 \(||\bm{e}||=1\);
-
按照特征值 从大到小 将对应的特征向量进行排序;
-
选择 特征值前 \(d^{'}\) 大 的特征向量作为投影向量,构成特征向量矩阵 \(Q \in \mathbb{R}^{d\times d^{'}}\) ,是一个标准正交矩阵;
-
对于任意的 \(d\) 维样本 \(\bm{x}_i\),用 \(PCA\) 降维后的 \(d^{'}\) 维向量为:
\[\bm{y}_i = Q^{\text{T}}(\bm{x}_i - \bm{\mu}) \]
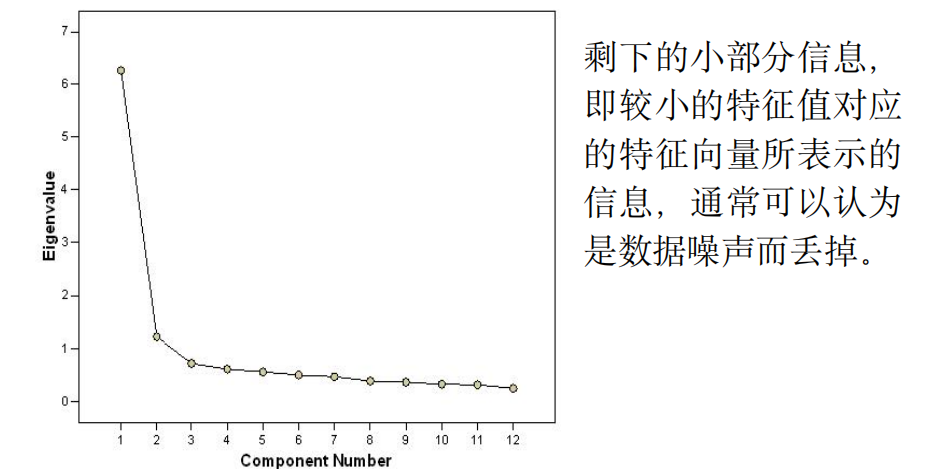
最大的几个特征值占据了所有特征值之和的绝大部分。将数据投影到少数几个最大特征值对应的特征向量方向上即可保留原数据中的绝大部分信息。样本投影到主成分上方差越大越能表明这个主成分能够更好地区分样本。
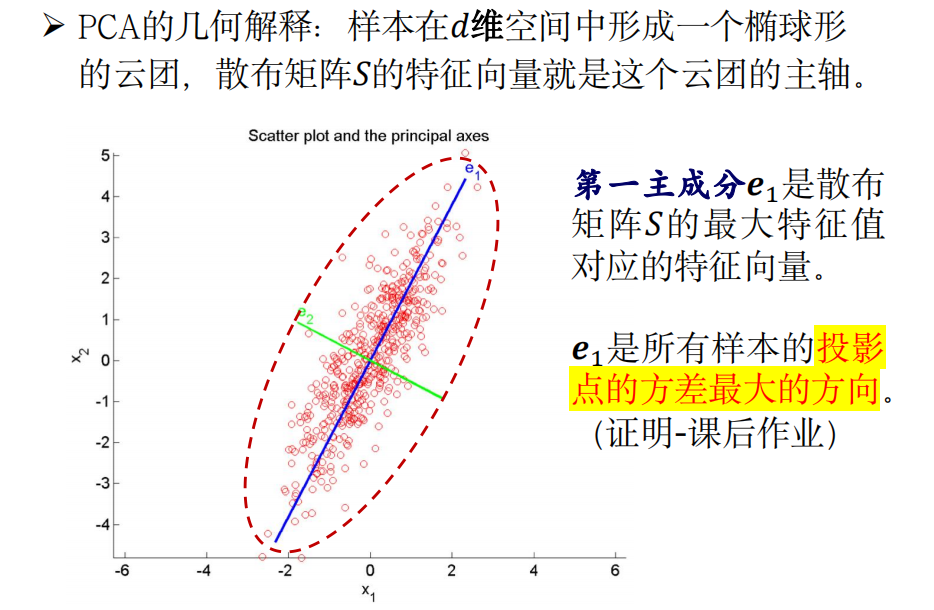
1.2 PCA 的几何解释
1.3 例题
例题 1
给定 \(d\) 维的样本集 \(D = \{ \bm{x}_1, \bm{x}_2, \ldots, \bm{x}_n \}\),\(\bm{\mu}\) 为均值向量。已知协方差矩阵为 \(\bm{\Sigma} = \frac{1}{n - 1}\sum_{i=1}^{n}(\bm{x}_i - \bm{\mu})(\bm{x}_i - \bm{\mu})^{\text{T}}\),散布矩阵为 \(S = \sum_{i=1}^{n}(\bm{x}_i - \bm{\mu})(\bm{x}_i - \bm{\mu})^{\text{T}}\)。
请分析在 \(\text{PCA}\) 中用协方差矩阵来代替散步矩阵是否会有影响,并证明。
解:
不产生影响。
设 \(\bm{e}\) 为协方差矩阵 \(\bm{\Sigma}\) 中特征值 \(\lambda\) 对应的特征向量,则有 \(\bm{\Sigma} \bm{e} = \lambda \bm{e}\)。
由于散布矩阵是协方差矩阵的 \(n - 1\) 倍,则有:
也即:
相当于 \(\bm{e}\) 是散布矩阵 \(S\) 中特征值 \((n-1)\lambda\) 对应的特征向量。
因此,协方差矩阵和散布矩阵下的 \(\text{PCA}\) 有着相同的特征向量,特征值是 \(n - 1\) 倍的关系(\(n - 1 > 0\)),不影响根据特征值大小对特征向量排序的结果,进而 不会产生影响。
例题 2
设原始数据集 \(D={\bm{x}_1, \bm{x}_2, \ldots , \bm{x}_n}\) 是 \(d\) 维的,采用 \(\text{PCA}\) 降维后,变成 \(k\) 维的,其中 \(k\le d\)。设 \(\text{PCA}\) 找到的 \(k\) 个主成分依次为 \(\bm{e}_1, \bm{e}_2, \ldots , \bm{e}_k\),则任意的 \(d\) 维样本 \(x\) 进行 \(\text{PCA}\) 降维后,在第 \(r\) 个主成分上的坐标为:\(\bm{e}_r^{\text{T}}(\bm{x} − \bm{\mu})\),其中 \(\bm{\mu} = \frac{1}{n}\sum_{i=1}^{n}\bm{x}_i\)。因此,第 \(i\) 个样本在第 \(r\) 个主成分上的投影点可以表示为 \(y_i = \bm{e}_r^{\text{T}}(\bm{x}_i − \bm{\mu})\),所以,所有样本在第 \(r\) 个主成分上的投影点依次为 \(y_1, y_2, \ldots, y_n\),共 \(n\) 个投影点。
请证明 \(\text{PCA}\) 的第一主成分就是所有样本投影到该方向上的投影点的方差最大的方向。
解:
-
计算 \(n\) 个投影点的均值 \(\bar{y}\):
\[\bar{y} = \frac{1}{n} \sum_{i=1}^{n} y_i = \frac{1}{n}\sum_{i=1}^{n} \bm{e}_r^{\text{T}}(\bm{x}_i - \bm{\mu}) = \bm{e}_r^{\text{T}}(\frac{1}{n}\sum_{i=1}^{n}\bm{x}_i - \bm{\mu}) = 0 \] -
计算 \(n\) 个投影点的方差:
\[\begin{split} Var &= \frac{1}{n - 1}\sum_{i=1}^{n}(y_i - \bar{y})^2 \\\\ &= \frac{1}{n - 1}\sum_{i=1}^{n}y_i^2 \\\\ &= \frac{1}{n - 1}\sum_{i=1}^{n}\bm{e}_r^{\text{T}}(\bm{x}_i - \bm{\mu})\bm{e}_r^{\text{T}}(\bm{x}_i - \bm{\mu}) \\\\ &= \frac{1}{n - 1}\sum_{i=1}^{n}\bm{e}_r^{\text{T}}(\bm{x}_i - \bm{\mu})(\bm{x}_i - \bm{\mu})^{\text{T}}\bm{e}_r \\\\ &= \bm{e}_r^{\text{T}}\bm{\Sigma}\bm{e}_r \end{split} \]其中 \(\bm{\Sigma}\) 为协方差矩阵:
\[\bm{\Sigma} = \frac{1}{n - 1}\sum_{i=1}^{n}(\bm{x}_i - \bm{\mu})(\bm{x}_i - \bm{\mu})^{\text{T}} \]由 \(\text{PCA}\) 中 \(\bm{\Sigma}\bm{e}_r = \lambda_r \bm{e}_r\),其中 \(\lambda_r\) 为第 \(r\) 大的特征值,故:
\[Var = \bm{e}_r^{\text{T}}\bm{\Sigma}\bm{e}_r = \lambda_r \bm{e}_r^{\text{T}}\bm{e}_r \]由于 \(||\bm{e}|| = 1\),得:
\[Var = \lambda_r \] -
由上述结论可得,所有样本在第 \(1\) 个主成分上得投影点得方差为 \(\lambda_1\),而 \(\lambda_1\) 是所有特征值中最大的。
故 \(\text{PCA}\) 第一主成分就是所有样本投影到该方向上的投影点的方差最大的方向。
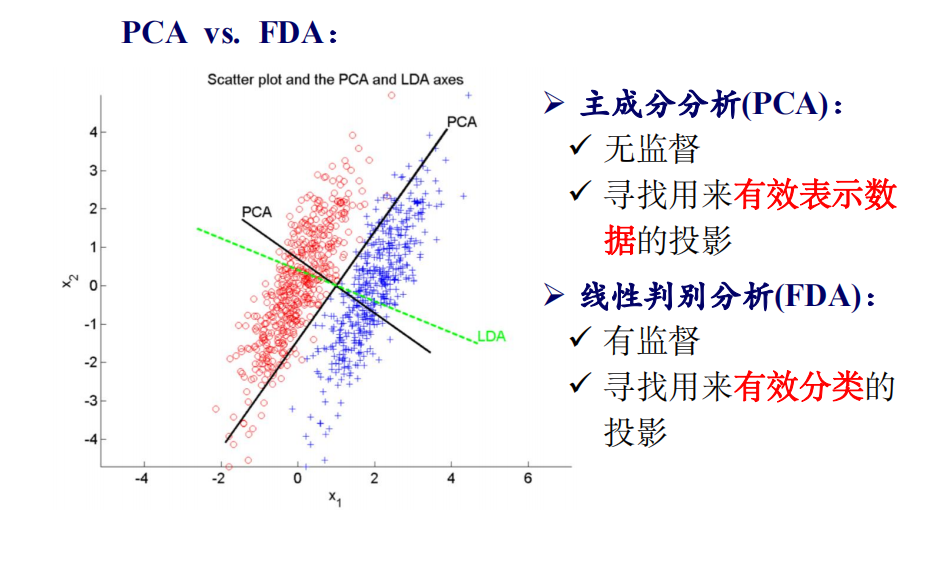
2. Fisher 线性判别分析 FDA
Fisher线性判别分析(FDA):寻找的是 能够有效分类 的方
向,是 有监督的降维方法。
Fisher判别分析 FDA