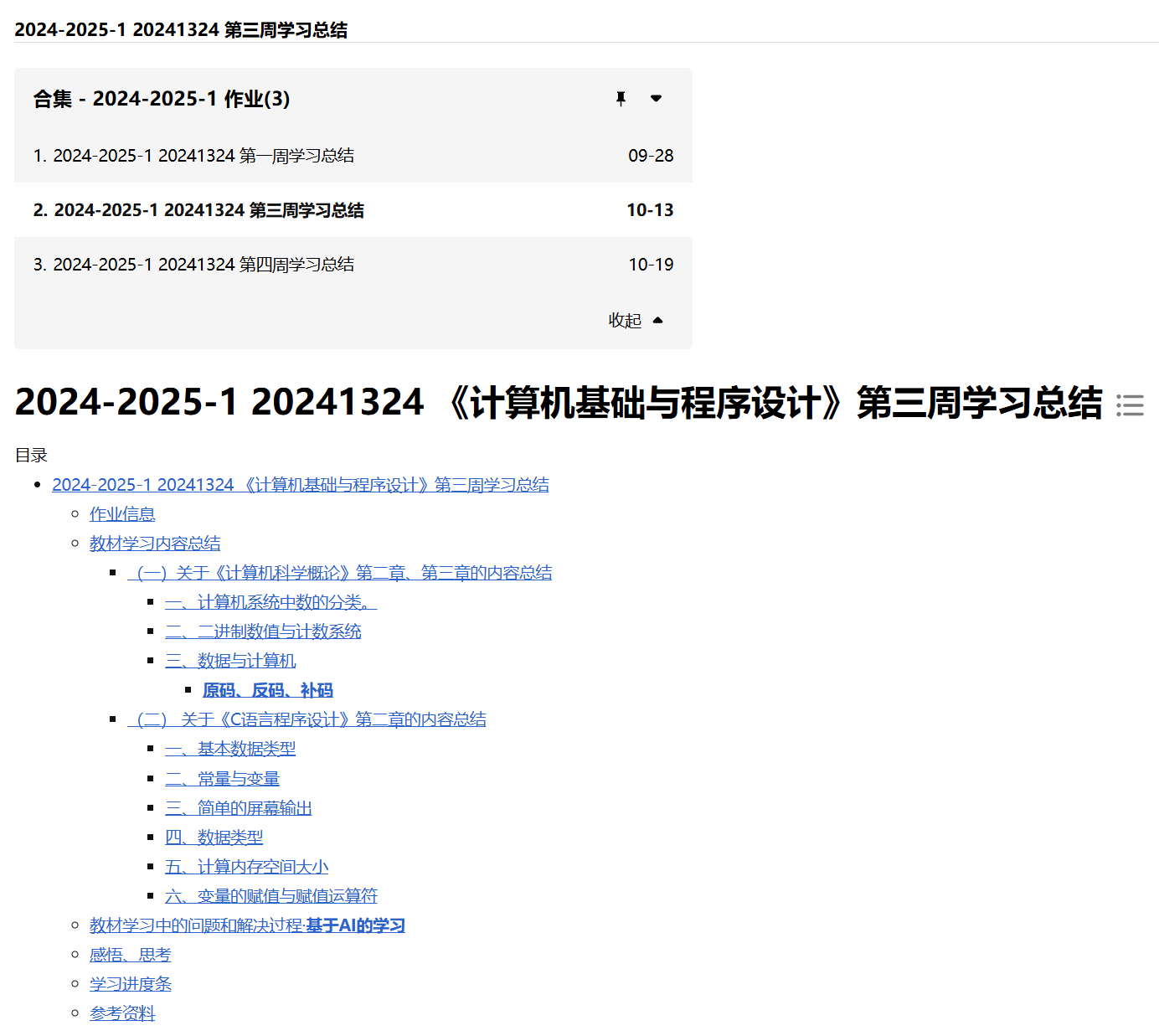
一、齐次方程
如果一阶微分方程可化成
\[\cfrac{\mathrm{d}y}{\mathrm{d}x} = \varphi \left( \cfrac{y}{x} \right) \tag{1}
\]
的形式,那么就称这方程为齐次方程。
在齐次方程
\[\cfrac{\mathrm{d}y}{\mathrm{d}x} = \varphi \left( \cfrac{y}{x} \right)
\]
中,引入新的未知函数
\[u = \cfrac{y}{x} \tag{2}
\]
就可以把它化为可分离变量的方程。因为由 \((2)\) 有
\[y = ux, \cfrac{\mathrm{d}y}{\mathrm{d}x} = u + x \cfrac{\mathrm{d}u}{\mathrm{d}x}
\]
代入方程 \((1)\) 便得方程
\[u + x \cfrac{\mathrm{d}u}{\mathrm{d}x} = \varphi(u)
\]
即
\[x \cfrac{\mathrm{d}u}{\mathrm{d}x} = \varphi(u) - u
\]
分离变量,得
\[\cfrac{\mathrm{d}u}{\varphi(u) - u} = \cfrac{\mathrm{d}x}{x}
\]
两端积分,得
\[\int \cfrac{\mathrm{d}u}{\varphi(u) - u} = \int \cfrac{\mathrm{d}x}{x}
\]
求出积分后,再以 \(\cfrac{y}{x}\) 代替 \(u\) ,便得所给齐次方程的通解。
例1 解方程 \(y^2 + x^2 \cfrac{\mathrm{d}y}{\mathrm{d}x} = xy \cfrac{\mathrm{d}y}{\mathrm{d}x}\) .
解:原方程可写成
\[\cfrac{\mathrm{d}y}{\mathrm{d}x} = \cfrac{y^2}{xy - x^2} = \cfrac{\left( \cfrac{y}{x} \right)^2}{\cfrac{y}{x} -1},
\]
因此是齐次方程。令 \(\cfrac{y}{x} = u\),则
\[y = ux, \cfrac{\mathrm{d}y}{\mathrm{d}x} = u + x \cfrac{\mathrm{d}u}{\mathrm{d}x}
\]
于是原方程变为
\[u + x \cfrac{\mathrm{d}u}{\mathrm{d}x} = \cfrac{u^2}{u - 1}
\]
即
\[x \cfrac{\mathrm{d}u}{\mathrm{d}x} = \cfrac{u}{u - 1}
\]
分离变量,得
\[\left( 1 - \cfrac{1}{u} \right) \mathrm{d}u = \cfrac{\mathrm{d}x}{x}
\]
两端积分,得
\[u - \ln |u| + C_1 = \ln |x|
\]
或写为
\[\ln |xu| = u + C_1
\]
以 \(\cfrac{y}{x}\) 代上式中的 \(u\) ,便得所给方程的通解为
\[\ln |y| = \cfrac{y}{x} + C_1 \quad 或 \quad y = C \mathrm{e}^{\frac{y}{x}} (C = \pm \mathrm{e}^{C_1}).
\]
*二、可化为齐次的方程
方程
\[\cfrac{\mathrm{d}y}{\mathrm{d}x} = \cfrac{ax + by + c}{a_1 x + b_1 y + c_1} \tag{3}
\]
当 \(c = c_1 = 0\) 时是齐次的,否则不是齐次的。在非齐次的情形,可用下列变换把它化为齐次方程:令
\[x = X + h, \quad y = Y + k,
\]
其中 \(h\) 及 \(k\) 是待定的常数。于是
\[\mathrm{d}x = \mathrm{d}X, \quad \mathrm{d}y = \mathrm{d}Y,
\]
从而方程 \((3)\) 成为
\[\cfrac{\mathrm{d}Y}{\mathrm{d}X} = \cfrac{aX + bY + ah + bk + c}{a_1X + b_1Y + a_1h + b_1k + c_1}
\]
如果方程组
\[\begin{equation*}\begin{cases}ah + bk + c = 0 \\a_1h + b_1k + c_1 = 0\end{cases}\end{equation*}
\]
的系数行列式 \(\left|\begin {array}{c} a&b \\ a_1&b_1 \end{array}\right| \neq 0\),即 \(\cfrac{a_1}{a} \neq \cfrac{b_1}{b}\) ,那么可以定出 \(h\) 及 \(k\) 使它们满足上述方程组。这样,方程 \((3)\) 便化为齐次方程
\[\cfrac{\mathrm{d}Y}{\mathrm{d}X} = \cfrac{aX + bY}{a_1X + b_1Y} .
\]
求出这齐次方程的通解后,在通解中以 \(x - h\) 代 \(X\) ,\(y - k\) 代 \(Y\) ,,便得方程 \((3)\) 的通解。
当 \(\cfrac{a_1}{a} = \cfrac{b_1}{b}\) 时,\(h\) 及 \(k\) 无法求得,因此上述方法不能应用。但这是令 \(\cfrac{a_1}{a} = \cfrac{b_1}{b} = \lambda\) ,从而方程 \((3)\) 可写成
\[\cfrac{\mathrm{d}y}{\mathrm{d}x} = \cfrac{ax + by + c}{\lambda (ax + by) + c_1} .
\]
引入新变量 \(v = ax + by\),则
\[\cfrac{\mathrm{d}v}{\mathrm{d}x} = a + b \cfrac{\mathrm{d}y}{\mathrm{d}x} \quad 或 \quad \cfrac{\mathrm{d}y}{\mathrm{d}x} = \cfrac{1}{b} \left( \cfrac{\mathrm{d}v}{\mathrm{d}x} - a \right) .
\]
于是方程 \((3)\) 称为
\[\cfrac{1}{b} \left( \cfrac{\mathrm{d}v}{\mathrm{d}x} - a \right) = \cfrac{v + c}{\lambda v + c_1} ,
\]
这是可分离变量的方程。
以上介绍的方法可以应用于更一般的方程
\[\cfrac{\mathrm{d}y}{\mathrm{d}x} = f \left( \cfrac{ax + by + c}{a_1x + b_1y + c_1} \right)
\]
例2 解方程 \((2x + y - 4) \mathrm{d}x + (x + y - 1)\mathrm{d}y = 0\) .
解:令 \(x = X + h, y = Y + k\) ,则 \(\mathrm{d}x = \mathrm{d}X, \mathrm{d}y = \mathrm{d}Y\) ,代入原方程得
\[(2X + Y + 2h + k - 4)\mathrm{d}X + (X + Y + h + k - 1)\mathrm{d}Y = 0
\]
解方程组
\[\begin{equation*}\begin{cases}2h + k - 4 = 0 \\h + k - 1 = 0\end{cases}\end{equation*}
\]
得 \(h = 3, k = -2\) .令 \(x = X + 3, y = Y - 2\),原方程成为
\[(2X + Y)\mathrm{d}X + (X + Y)\mathrm{d}Y = 0
\]
或
\[\cfrac{\mathrm{d}Y}{\mathrm{d}X} = - \cfrac{2X + Y}{X + Y} = - \cfrac{2 + \cfrac{Y}{X}}{1 + \cfrac{Y}{X}} ,
\]
这是齐次方程。
令 \(\cfrac{Y}{X} = u\) ,则 \(Y = Xu, \cfrac{\mathrm{d}Y}{\mathrm{d}X} = u + X \cfrac{\mathrm{d}u}{\mathrm{d}X}\) ,于是方程变为
\[u + X \cfrac{\mathrm{d}u}{\mathrm{d}X} = - \cfrac{2 + u}{1 + u} ,
\]
或
\[X \cfrac{\mathrm{d}u}{\mathrm{d}X} = - \cfrac{2 + 2u + u^2}{1 + u} .
\]
分离变量得
\[\cfrac{\mathrm{d}X}{X} = - \cfrac{u + 1}{2 + 2u + u^2} \mathrm{d}u .
\]
积分得
\[\ln C_1 - \cfrac{1}{2} \ln{(u^2 + 2u + 2)} = \ln |X| ,
\]
于是
\[\cfrac{C_1}{\sqrt{u^2 + 2u + 2}} = |X|
\]
或
\[C_2 = X^2 (u^2 + 2u + 2) \quad (C_2 = C_1^2) ,
\]
即
\[Y^2 + 2XY + 2X^2 = C_2 .
\]
以 \(X = x - 3, Y = y + 2\) 代入上式并化简,得
\[2x^2 + 2xy + y^2 - 8x - 2y = C \quad (C = C_2 - 10).
\]