NZOJ 模拟赛6

T1 叉叉

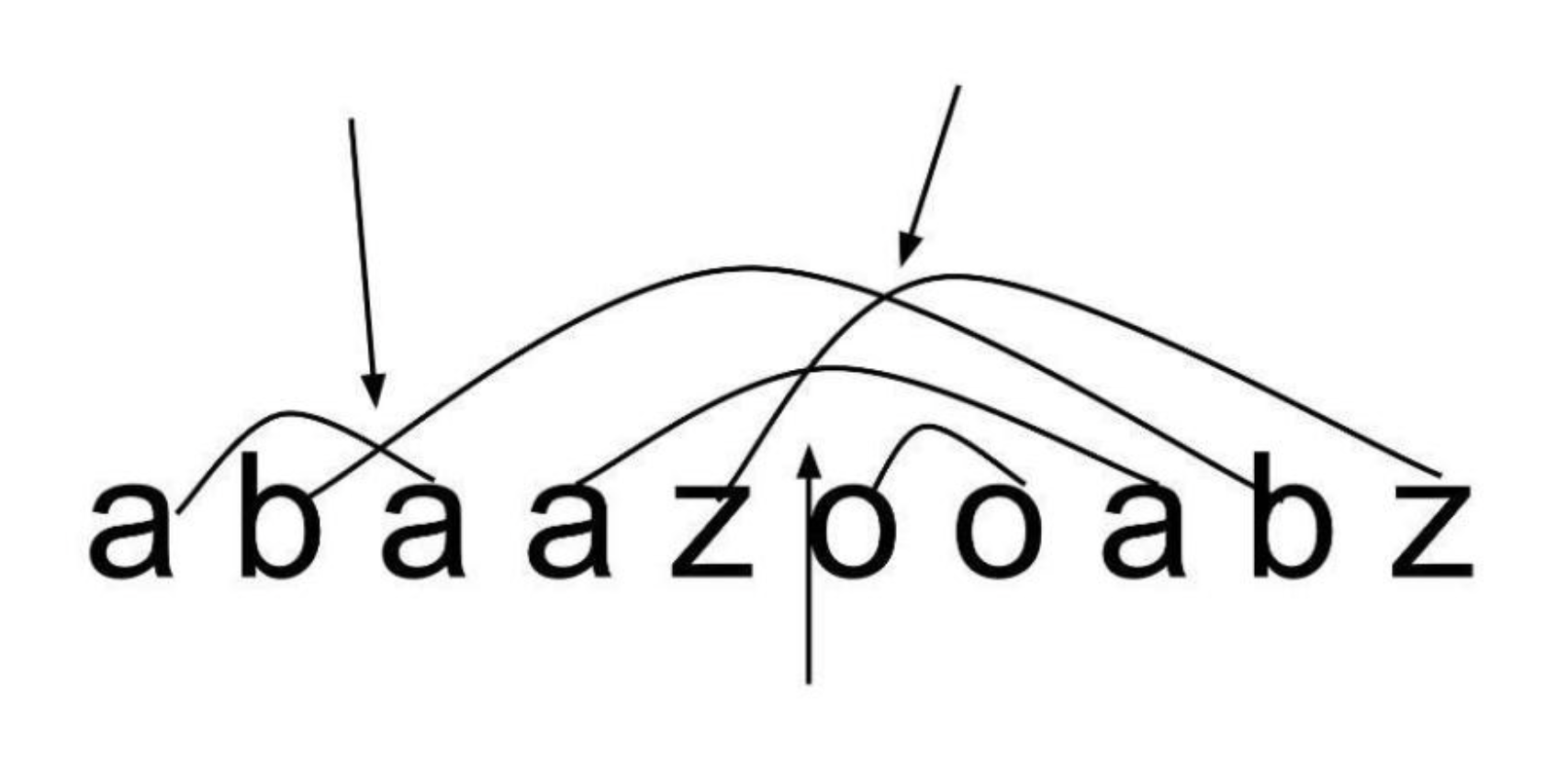
现在有一个字符串，每个字母出现的次数均为偶数。接下来我们把第一次出现的字母a和第二次出现的a连一条线，第三次出现的和四次出现的字母a连一条线，第五次出现的和六次出现的字母a连一条线...对其他25个字母也做同样的操作。

现在我们想知道有多少对连线交叉。交叉的定义为一个连线的端点在另外一个连线的内部，另外一个端点在外部。

下图是一个例子，共有三对连线交叉（我们连线的时候，只能从字符串上方经过）。

一行一个字符串。保证字符串均由小写字母组成，且每个字母出现次数为偶数次。

对于100%的数据，字符串长度不超过100,000。

事实上 \(O(n^2)\) 的暴力都能够通过此题，也许是字符集过小使得期望复杂度优化到了 \(O(n\sigma)\)，如果 \(\sigma\) 够大这样的算法就无法通过，所以我们来谈谈正解。

我们来考虑整个字符串匹配的过程，可以得到许多个字符串，你想要求有多少对字符串相交了，从左到右的扫描过程中，我们每遇到一个左端点，存入 \(last\) 数组中，下次遇到右端点的时候清空 \(last\)，并且遇到左端点，对后继答案贡献 \(+1\)，遇到右端点对后继答案 \(-1\)。

这样操作的一个好处是，我们只考虑的单侧的答案，因此对于两条线段相交，一定不会被重复统计两次，接下来考虑处理答案的问题。

匹配过程中，对于当前线段 \([l, ~ r]\)，考虑对 \([l, ~ r]\) 内未被匹配的点的数量求和，因此我们可以用树状数组来优化。

当遇到线段的左端点时，在左端点处 \(+1\)，遇到右端点时，在左端点处 \(-1\)，每次匹配后求出 \([l, ~ r]\) 的子段和即可。

时间复杂度 \(O(n\log{n})\)。

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N = 1e5 + 10;
int n, last[26];
int tr[N];
ll ans;
char a[N];int lowbit(int x)
{return x & -x;
}void add(int x, int d)
{for (int i = x; i <= n; i += lowbit(i)) tr[i] += d;
}int sum(int x)
{int res = 0;for (int i = x; i; i -= lowbit(i)) res += tr[i];return res;
}int main()
{cin >> (a + 1), n = strlen(a + 1);for (int i = 1; i <= n; i ++ ){if (last[a[i] - 'a']){add(last[a[i] - 'a'], -1);ans += sum(i) - sum(last[a[i] - 'a']);last[a[i] - 'a'] = 0;}else last[a[i] - 'a'] = i, add(i, 1);}cout << ans;return 0;
}

T2 跳跳虎回家

跳跳虎在外面出去玩忘了时间，现在他需要在最短的时间内赶回家。
跳跳虎所在的世界可以抽象成一个含有n个点的图（点编号从1到n），跳跳虎现在在1号点，跳跳虎的家在n号点。
图上一共有m条单向边，通过每条边有固定的时间花费。
同时，还存在若干个单向传送通道，传送通道也有其时间花费。
传送通道一般来说比普通的道路更快，但是跳跳虎最多只能使用k次。
跳跳虎想知道他回到家的最小时间消耗是多少。

第一行输入4个整数n,m,q,k。（n表示点数，m表示普通道路的数量，q表示传送通道的数量，k表示跳跳虎最多使用k次传送通道）
接下来m行每行3个整数u,v,w，表示有一条从u到v，时间花费为w的普通道路。(1≤u,v≤n,1≤w≤10^3)
接下来q行每行3个整数x,y,z，表示有一条从x到y，时间花费为z的传送通道。(1≤x,y≤n,1≤z≤10^3)

对于100%的数据，1≤n≤500,0≤m,q≤2000,0≤k≤10^9。

考虑建立一个分层图模型，什么是分层图呢？

在原有图的基础上，我们将这个图复制多次，产生一个层状结构，每次利用通道相当于向下一层，最多经历 \(k\) 层就可以到达底部，由于 \(q \le 2000\)，因此 \(k\) 取得再大也超过 \(q\) 也是无效的，因为对于同一个通道，我使用两次一定是不优的，于是可以写出本题代码。

#include<bits/stdc++.h>
using namespace std;
typedef pair<int, int> PII;
const int N = 1e6 + 1000, INF = 0x7f7f7f7f;
int n, m, q, t;
int h[N], e[N << 4], ne[N << 4], w[N << 4], idx;
int dist[N], st[N];void add(int a, int b, int c)
{e[idx] = b, w[idx] = c, ne[idx] = h[a], h[a] = idx ++ ;
}void dijkstra(int S)
{memset(dist, 0x7f, sizeof dist);priority_queue<PII, vector<PII>, greater<PII>> heap;heap.push({0, S}), dist[S] = 0;while (heap.size()){PII t = heap.top();heap.pop();int u = t.second, d = t.first;if (st[u]) continue;st[u] = 1;for (int i = h[u]; ~i; i = ne[i]){int j = e[i];if (dist[j] > d + w[i]){dist[j] = d + w[i];heap.push({dist[j], j});}}}
}int main()
{memset(h, -1, sizeof h);scanf("%d%d%d%d", &n, &m, &q, &t);t = min(q, t);for (int i = 1; i <= m; i ++ ){int a, b, c;scanf("%d%d%d", &a, &b, &c);for (int j = 0; j <= t; j ++ )add(a + j * n, b + j * n, c);}for (int i = 1; i <= q; i ++ ){int a, b, c;scanf("%d%d%d", &a, &b, &c);for (int j = 0; j < t; j ++ )add(a + j * n, b + (j + 1) * n, c);}dijkstra(1);int ans = INF;for (int i = 0; i <= t; i ++ ) ans = min(ans, dist[n * (i + 1)]);if (ans == INF) ans = -1;printf("%d", ans);return 0;
}

然后兴高采烈地交一发，美妙的 TLE 了，用了 1.2s，推测可能是将整个图建出来后 \(n\) 太大，导致 dijkstra 的 \(O(n\log{n})\) 复杂度常数太大。

我们考虑在原图上跑 dijkstra，记录 \(dist[i][j]\) 表示到 \(i\) 点用了 \(j\) 次快速通道的最短路，常数可以变小，因而可以通过此题。

为了实现这个我们需要将边分类为两种，跑第一种的时候考虑同层最短路，跑第二种的时候考虑向下转移，\(st\) 数组开到二维即可，具体实现如下。

#include<bits/stdc++.h>
using namespace std;
typedef pair<int, int> PII;
typedef pair<int, PII> PPI;
const int N = 510, M = 2010, INF = 0x7f7f7f7f;
int n, m, q, t;
int h[N], is[M << 1], e[M << 1], ne[M << 1], w[M << 1], idx;
int dist[N][M], st[N][M];void add(int a, int b, int c, int d)
{e[idx] = b, w[idx] = c, is[idx] = d, ne[idx] = h[a], h[a] = idx ++ ;
}void dijkstra(int S)
{memset(dist, 0x7f, sizeof dist);priority_queue<PPI, vector<PPI>, greater<PPI>> heap;heap.push({0, {S, 0}}), dist[S][0] = 0;while (heap.size()){PPI top = heap.top();heap.pop();int u = top.second.first, d = top.first, k = top.second.second;if (st[u][k]) continue;st[u][k] = 1;for (int i = h[u]; ~i; i = ne[i]){int j = e[i];if (!is[i]){if (dist[j][k] > d + w[i]){dist[j][k] = d + w[i];heap.push({dist[j][k], {j, k}});}}else if (k < t){if (dist[j][k + 1] > d + w[i]){dist[j][k + 1] = d + w[i];heap.push({dist[j][k + 1], {j, k + 1}});}}}}
}int main()
{memset(h, -1, sizeof h);scanf("%d%d%d%d", &n, &m, &q, &t);t = min(q, t);for (int i = 1; i <= m; i ++ ){int a, b, c;scanf("%d%d%d", &a, &b, &c);add(a, b, c, 0);}for (int i = 1; i <= q; i ++ ){int a, b, c;scanf("%d%d%d", &a, &b, &c);add(a, b, c, 1);}dijkstra(1);int ans = INF;for (int i = 0; i <= t; i ++ ) ans = min(ans, dist[n][i]);if (ans == INF) ans = -1;printf("%d", ans);return 0;
}

事实上这个也跑了 700ms，小卡了一波常数，不过分层图的思想是需要掌握的。

时间复杂度 \(O((n + m + q)\min{(k, ~ q)}\log{(m + q)})\)。

T3 树

给定一棵n个节点，以S为根的树，边有权，删掉一条边的代价为这条边的边权。现在你要删除若干条边，使得根节点S不能到达任何叶子节点。请求出最小的代价和。

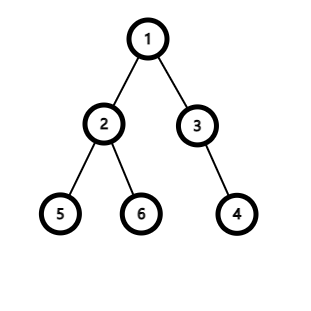
设 \(dp[i]\) 表示以 \(i\) 为根的子树无法到达任何叶子节点的最小代价，考虑如何向父亲转移。

可以发现，父亲 \(u\) 无法到达该子树的任何叶子结点的最小代价应该为 \(\min{(dp[i], w[u][i])}\)，其中 \(w[u][i]\) 表示 \(u \to i\) 的边权。

那么 \(dp[u]\) 可以很快得到 \(dp[u] = \sum\limits_{i \in son[u]} \min{(dp[i], w[u][i])}\)。

只需要初始化叶子节点为 \(inf\)，所有其他节点为 \(0\) 即可。

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N = 1e5 + 10;
int n, S;
int h[N], e[N << 1], ne[N << 1], idx;
ll w[N << 1], dp[N];void add(int a, int b, ll c)
{e[idx] = b, w[idx] = c, ne[idx] = h[a], h[a] = idx ++ ;
}void dfs(int u, int f)
{if (ne[h[u]] == -1 && e[h[u]] == f) return dp[u] = 1e18, void();for (int i = h[u]; ~i; i = ne[i]){int j = e[i];if (j == f) continue;dfs(j, u);dp[u] += min(w[i], dp[j]);}
}int main()
{cin >> n >> S;memset(h, -1, sizeof h);for (int i = 1; i < n; i ++ ){int a, b;ll c;cin >> a >> b >> c;add(a, b, c), add(b, a, c);}dfs(S, 0);cout << dp[S];return 0;
}

T4 阶乘

求出n的阶乘在k进制表示下末尾0的个数。

对于100%的数据，\(n \le 10^{12}, ~ k \le 10^{12}\)。

考虑如何在 \(k\) 进制下出现 \(0\)，那必然是可以将 \(n\) 表示为 \(N \times k^t(N, ~ k, ~ t \in N^*)\) 的形式，我们需要求出这个 \(t\)。

我们可以考虑将 \(k\) 质因数分解为 \(k = p_{1}^{\alpha_1}p_{2}^{\alpha_2}...p_{s}^{\alpha_s}\)。

现在问题就转化为求这些质数在 \(n!\) 中出现了多少次了。

让我们介绍勒让德定理。

在 \(n!\) 的唯一分解中，对于质数 \(p\)，记 \(L_p(n!)\) 为素数 \(p\) 的最高指数，这里的 \(L_p(n!)\) 为勒让德函数。

勒让德定理：

\[L_p(n!) = \sum_{k \ge 1}\bigg\lfloor\frac{n}{p^k}\bigg\rfloor \]

证明：

记 \(N_p(n!, ~ k)\) 表示 \([1, ~ n!]\) 中唯一分解后素数 \(p\) 的幂为 \(k\) 的数个数。

易知 \(L_p(n!) = N_p(n!, ~ 1) + 2N_p(n!, ~ 2) + ... + rN_p(n!, ~ r)\)。

而对于 \([1, n]\) 中能被 \(p\) 整除的数有 \(\lfloor\frac{n}{p}\rfloor\) 个，即 \(N_p(n!, ~ 1) + N_p(n!, ~ 2) + ... + N_p(n!, ~ r)\) 个。

对于 \([1, n]\) 中能被 \(p^k\) 整除的数有 \(\lfloor\frac{n}{p^k}\rfloor\) 个，即 \(N_p(n!, ~ k) + N_p(n!, ~ k + 1) + ... + N_p(n!, ~ r)\) 个。

综上可知：

\[\begin{aligned}L_p(n!) &= N_p(n!, ~ 1) + 2N_p(n!, ~ 2) + ... + rN_p(n!, ~ r)\\&= \sum\limits_{k \ge 1}\bigg\lfloor\frac{n}{p^k}\bigg\rfloor\end{aligned}\]

证毕。

因此此题我们找出 \(k = p_{1}^{\alpha_1}p_{2}^{\alpha_2}...p_{s}^{\alpha_s}\) 中，对任意 \(p_i\) 求 \(L_{p_i}(n!)\)，将 \(L_{p_i}(n!)\) 个 \(p_i\) 分配到 \(k\) 上，每 \(\alpha_i\) 个 \(p_i\) 可能产生一个 \(k\) 的因子，即对末尾 \(0\) 做出贡献。

所以我们的答案为表达式如下：

\[ans = \min_{i = 1}^{s}\bigg\lfloor\frac{L_{p_i}(n!)}{\alpha_i}\bigg\rfloor \]

分解 \(k\) 需要注意可能有大素数，分解出 \(\sqrt{k}\) 以下的质数后特判以下即可。

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N = 1e6 + 10;
ll n, k, ans = 1e12;
ll primes[N], num[N], cnt;
bool st[N];void init(int n)
{for (int i = 2; i <= n; i ++ ){if (!st[i]) primes[ ++ cnt] = i;for (int j = 1; primes[j] <= n / i; j ++ ){st[primes[j] * i] = 1;if (i % primes[j] == 0) break;}}
}int main()
{cin >> n >> k;init(sqrt(k));for (int i = 1; i <= cnt; i ++ )while (k % primes[i] == 0)k /= primes[i], num[i] ++ ;for (int i = 1; i <= cnt; i ++ ){ll res = 0;if (num[i]){ll t = 1;while (n / primes[i] >= t)t *= primes[i], res += n / t;ans = min(ans, res / num[i]);}}ll res = 0;if (k != 1) {ll t = 1;while (n / k >= t)t *= k, res += n / t;ans = min(ans, res);}cout << ans;return 0;
}