资本（生成函数）

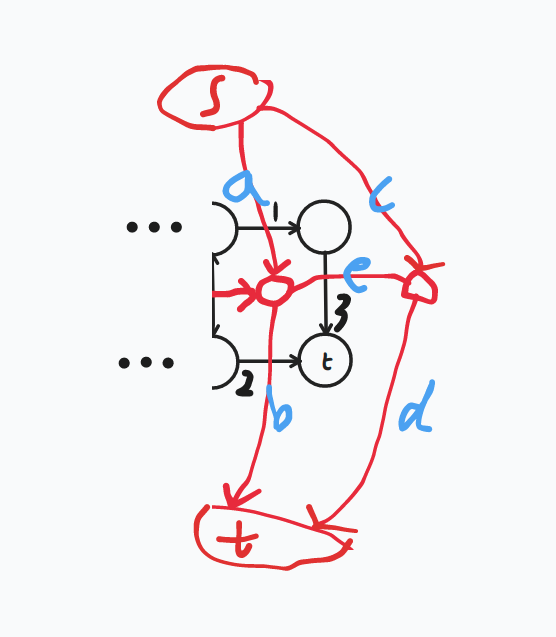
$\quad $ 其中 $n\le 1e3 $ 、$ m\le 1e9 $ 、 $ T\le 10 $。

$\quad $ 这是一个排列问题，所以我们可以考虑指数型生成函数，这里我们称 \(x ^n\) 的系数为 \(\frac{x ^n}{n!}\) 之前的系数，下文记作 \([x ^n]\) 。

$\quad $ 我们定义函数 \(f _{k}(x)=\sum _{n=0}^{k}\frac{x ^n}{n!}\) ，那么 \([x^n]\) 表示选其中 \(n\) 个数（可重复）且该数出现次数不超过 \(k\) 时的合法方案数。

$\quad $ 那么 \([x^n]e _{k}^{m}(x)\) 就表示在 \(m\) 个数中选出 \(n\) 个数（可重），使得每个选出的数出现次数都不超过 \(k\) 的方案数。

$\quad $ 那么 \([x^n]e_{k}^{m}(x)-[x^n]e _{k-1}^{m}(x)\) 就表示在 \(m\) 个数中选出 \(n\) 个数（可重），使得众数为 \(k\) 的方案数。

下文 \([x^n]\) 代指 \(x^n\) 之前的系数。

$\quad $ 答案就是：

\[n!\sum _{k=1}^{n}k([x^n]e ^{m}_{k}(x)-[x^n]e ^{m}_{k-1}(x)) \]

再化简一下：

\[n!(n[x^n]e ^{m}_{n}(x)-\sum _{k=1}^{n-1}[x^n]e ^{m} _{k}(x)) \]

$\quad $ 现在再考虑求出 \([x^n]e _{k}^{m}(x)\)

首先对 \(e ^m_{k}(x)\) 求导，这里用到了复合函数的求导，（简单写了，不是很严谨）即：

对于两个函数 \(f(x)、g(x)\) ，令 \(h(x)=f[g(x)]\) ，则 \(h'(x)=f'[g(x)] g'(x)\)

书上给的

如果 \(u=g(x)\) 在点 \(x\) 处可导，而 \(y=f(u)\) 在点 \(u=g(x)\) 处可导，那么复合函数 \(y=g[f(x)]\) 在点 \(x\) 处可导，且其导数为

\[\frac{dy}{dx}=f'(u)\cdot g'(x) \]

这里我们可以把 \(e ^m_{k}(x)\) 看做是 $f(x)=x^m $ 和 \(g(x)=e _{k}(x)\) 的复合函数

那么：

\[(e ^{m}_{k}(x))'=me ^{m-1}_{k}(x)e'_{k}(x) \]

现在看看 \(e'_{k}(x)\) ，因为 \(e _{k}(x)=\sum _{i=0}^{k}\frac{x^i}{i!}\) ，故 \(e'_{k}(x)=\sum _{i=1}^{k}\frac{x ^{i-1}}{(i-1)!}=\sum _{i=0}^{k-1}\frac{x^i}{i!}=e _{k}(x)-\frac{x^k}{k!}\) 。

所以：
\begin{aligned}
(e ^{m}_{k}(x))'&=me ^{m-1} _{k}(x) e' _{k} (x)\\
&=me ^{m-1} _{k}(x)(e _{k} ^{m}(x)-\frac{x ^k}{k!})\\
&=m e ^{m} _{k}(x)-\frac{mx ^k}{k!}e _{k} ^{m-1}(x)\\
\end{aligned}

那么对于其 \(n\) 次项系数，该等式仍然成立。

也就是：

\[[x^n](e ^{m}_{k}(x))'=[x^n]m e ^{m} _{k}(x)-\frac{mx ^k}{k!}[x ^{n-k}]e _{k} ^{m-1}(x) \]

此时设 \(e _{k} ^{m}(x)=\sum _{n=0}^{m}A(n,m)x^n\) ，那么可知 \([x^n](e ^{m}_{k}(x))' =(n+1)A(n+1,m)\)

于是：

\[(n+1)A(n+1,m)=mA(n,m)-\frac{m}{k!}A(n-k,m-1) \]

$\quad $ 再化成我们熟悉的递推式：

\[iA(i,j)=jA(i-1,j)-\frac{j}{k!}A(i-k-1,j-1) \]

$\quad $ 当 \(m=1\) 时，该式的值为 \(\frac{1}{n!}\) ， \(n=0\) 时，该式的值为 \(1\) ， \(n\le 0\) 时则为 \(0\) 。

然后愉快递推就好了，时间复杂度 \(O(n ^2 log n)\)

点击查看代码

#include<bits/stdc++.h>
#define int long long
const int N=1e3+10,p=1e9+7;
int fact[N],n,m,t,ny[N],nyp[N],k,f[N][N];
inline int qum(int a,int b){int ans=1;while(b){(b&1)&&(ans=ans*a%p);a=a*a%p;b>>=1;}return ans;
}
signed main(){// freopen("1.in","r",stdin);freopen("capital.in","r",stdin);freopen("capital.out","w",stdout);scanf("%lld",&t);fact[0]=1;for(int i=1;i<=1000;i=-~i)fact[i]=fact[i-1]*i%p;ny[1000]=qum(fact[1000],p-2);for(int i=999;i;i--)ny[i]=ny[i+1]*(i+1)%p;for(int i=1;i<=1000;i=-~i)nyp[i]=fact[i-1]*ny[i]%p;while(t--){scanf("%lld%lld",&n,&m);int ans=0;for(int i=1;i<=n+1;i++)f[0][i]=1;for(k=1;k<=n;k=-~k){f[k][1]=ny[k];int op=n/k+1,d=m-op;for(int i=1;i<=op;i=-~i){for(int j=1;j<=k;j=-~j){f[j][i]=nyp[j]*(i+d)%p*f[j-1][i]%p;}for(int j=k+1;j<=n;j++){f[j][i]=nyp[j]*(i+d)%p*(f[j-1][i]-ny[k]*f[j-k-1][i-1]%p+p)%p;}}ans=(k^n)?(ans+f[n][m-d])%p:(n*f[n][m-d]%p-ans+p)%p;}ans=ans*fact[n]%p;printf("%lld\n",ans);}
}

《唐完了》，5k一语惊醒梦中人。