快速范围判断
经常要批量判断某些值在不在范围内,如果 int 检测是 [0, N) 的话:
if (x >= 0 && x < N) ...
众所周知,现代 CPU 优化,减分支是重要手段,上述两次判断可以简写为:
if (((unsigned int)x) < N) ...
减少判断次数。如果 int 检测范围是 [minx, maxx] 这种更常见的形式的话,怎么办呢?
if (x >= minx && x <= maxx) ...
可以继续用比特或操作继续减少判断次数:
if (( (x - minx) | (maxx - x) ) >= 0) ...
如果语言警察们担心有符号整数回环是未定义行为的话,可以写成这样:
if ((int32_t)(((uint32_t)x - (uint32_t)minx) | ((uint32_t)maxx - (uint32_t)x)) > = 0) ...
性能相同,但避开了有符号整数回环,改为无符号回环,合并后转为有符号判断最高位。
第一个 (x - minx) 如果 x < minx 的话,得到的结果 < 0 ,即高位为 1,第二个判断同理,如果超过范围,高位也为 1,两个条件进行比特或运算以后,只有两个高位都是 0 ,最终才为真,同理,多个变量范围判断整合:
if (( (x - minx) | (maxx - x) | (y - miny) | (maxy - y) ) >= 0) ...
这样本来需要对 [x, y] 进行四次判断的,可以完全归并为一次判断,减少分支。
补充:加了个性能评测:
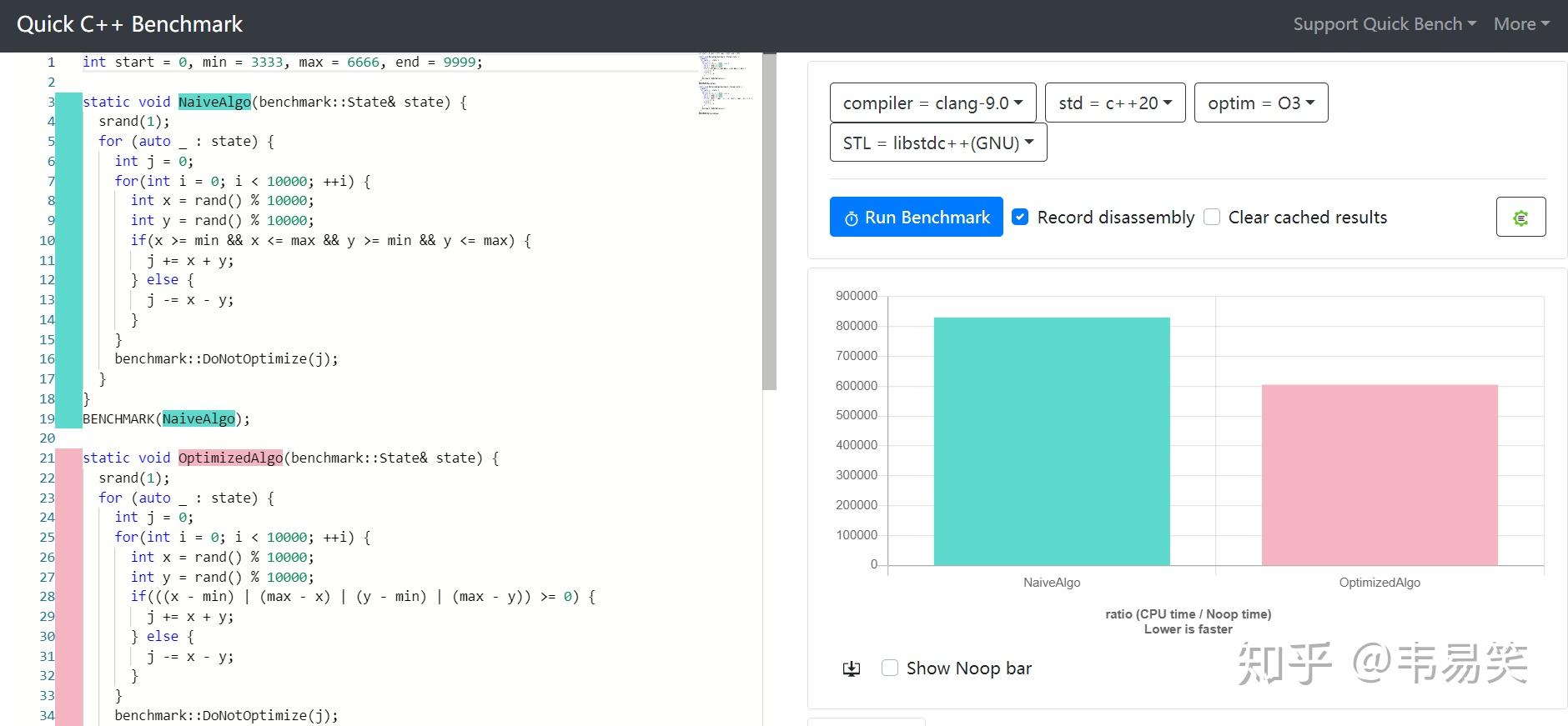
性能提升 37%。快速范围判断还有第二个性能更均衡的版本:
if ((unsigned)(x - minx) <= (unsigned)(maxx - minx)) ...
快速范围判断的原理和评测详细见:《快速范围判断:再来一种新写法》。
更好的循环展开
很多人提了 duff's device ,按照 gcc 和标委会丧心病狂的程度,你们用这些 just works 的代码,不怕哪天变成未定义行为给一股脑优化掉了么?其实对于循环展开,可以有更优雅的写法:
#define CPU_LOOP_UNROLL_4X(actionx1, actionx2, actionx4, width) do { \unsigned long __width = (unsigned long)(width); \unsigned long __increment = __width >> 2; \for (; __increment > 0; __increment--) { actionx4; } \if (__width & 2) { actionx2; } \if (__width & 1) { actionx1; } \
} while (0)
送大家个代替品,CPU_LOOP_UNROLL_4X,用于四次循环展开,用法是:
CPU_LOOP_UNROLL_4X({*dst++ = (*src++) ^ 0x80;},{*(uint16_t*)dst = (*(uint16_t*)src) ^ 0x8080;dst += 2; src += 2;},{*(uint32_t*)dst = (*(uint32_t*)src) ^ 0x80808080;dst += 4; src += 4;},w);
假设要对源内存地址内所有字节 xor 0x80 然后复制到目标地址的话,可以向上面那样进行循环展开,分别写入 actionx1, actionx2, actionx4 即:单倍工作,双倍工作,四倍工作。然后主体循环将用四倍工作的代码进行循环,剩余长度用两倍和单倍的工作拼凑出来。
现在的编译器虽然能够帮你展开一些循环,CPU 也能对短的紧凑循环有一定预测,但是做的都非常傻,大部分时候你用这样的宏明确指定循环展开循环效果更好,你还可以再优化一下,主循环里每回调用两次 actionx4,这样还能少一半循环次数,剩余的用其他拼凑。
这样比 duff's device 这种飞线的写法更规范,并且,duff's device 并不能允许你针对 “四倍工作”进行优化,比如上面 actionx4 部分直接试用 uint32_t 来进行一次性运算,在 duff's device 中并没有办法这么做。
补充:《循环展开性能评测》:
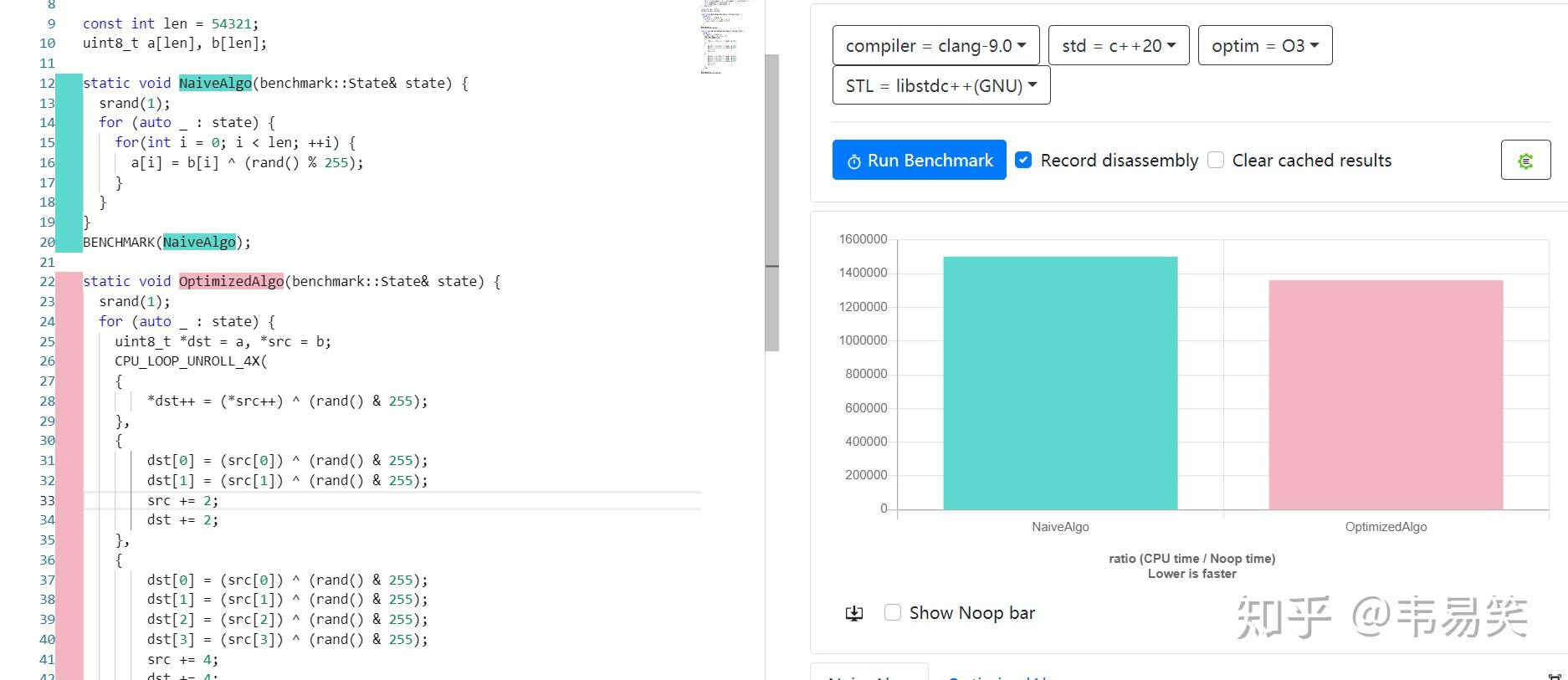
性能提升 12% 。
整数快速除以 255
整数快速除以 255 这个事情非常常见,例如图像绘制/合成,音频处理,混音计算等。网上很多比特技巧,却没有人总结过非 2^n 的快速除法方法,所以我自己研究了个版本:
#define div_255_fast(x) (((x) + (((x) + 257) >> 8)) >> 8)
当 x 属于 [0, 65536] 范围内,该方法的误差为 0。过去不少人简略的直接用 >> 8 来代替,然而这样做会有误差,连续用 >>8 代替 / 255 十次,误差就累计到 10 了。
上面的宏可以方便的处理 8-16 位整数的 /255 计算,经过测试 65536000 次计算中,使用 /255的时间是 325ms,使用div_255_fast的时间是70ms,使用 >>8 的时间是 62ms,div_255_fast 的时间代价几乎可以忽略。
进一步可以用 SIMD 写成:
// (x + ((x + 257) >> 8)) >> 8
static inline __m128i _mm_fast_div_255_epu16(__m128i x) {return _mm_srli_epi16(_mm_adds_epu16(x, _mm_srli_epi16(_mm_adds_epu16(x, _mm_set1_epi16(0x0101)), 8)), 8);
}
这样可以同时对 8 对 16 bit 的整数进行 / 255 运算,照葫芦画瓢,还可以改出一个 / 65535 ,或者 / 32767 的版本来。
对于任意大于零的整数,他人总结过定点数的方法,x86 跑着一般,x64 下还行:
static inline uint32_t fast_div_255_any (uint32_t n) {uint64_t M = (((uint64_t)1) << 32) / 255; // 用 32.32 的定点数表示 1/255return (M * n) >> 32; // 定点数乘法:n * (1/255)
}
这个在所有整数范围内都有效,但是精度有些不够,所以要把 32.32 的精度换成 24.40 的精度,并做一些四舍五入和补位:
static inline uint32_t fast_div_255_accurate (uint32_t n) {uint64_t M = (((uint64_t)1) << 40) / 255 + 1; // 用 24.40 的定点数表示 1/255return (M * n) >> 40; // 定点数乘法:n * (1/255)
}
该方法能够覆盖所有 32 位的整数且没有误差,有些编译器对于常数整除,已经可以生成类似 fast_div_255_accurate 的代码了,整数除法是现代计算机最慢的一项工作,动不动就要消耗 30 个周期,常数低的除法除了二次幂的底可以直接移位外,编译器一般会用定点数乘法模拟除法。
编译器生成的常数整除代码主要是使用了 64 位整数运算,以及乘法,略显复杂,对普通 32 位程序并不是十分友好。因此如果整数范围属于 [0, 65536] 第一个版本代价最低。
且 SIMD 没有除法,如果想用 SIMD 做除法的话,可用上面的两种方法翻译成 SIMD 指令。
255 快除法的《性能评测》:
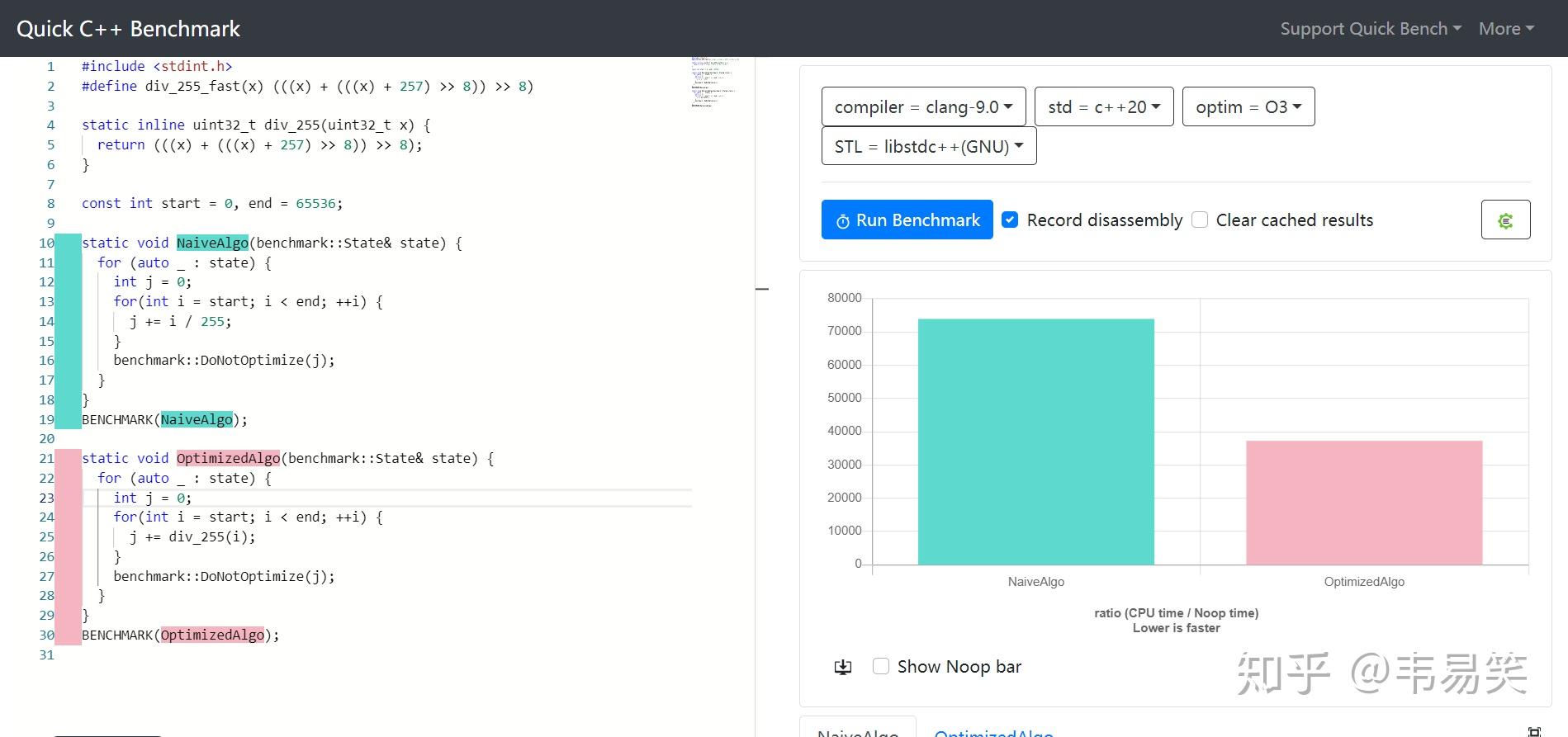
提升一倍的性能。
PS:大部分时候当然选择相信编译器,提高可读性,如果你只写一些增删改查,那怎么漂亮怎么写就行;但如果你想写极致性能的代码,你需要知道编译器的优化是有限的穷举,没法应对无限的代码变化,上面三个就是例子,编译器优化可以帮你,但没法什么都靠编译器,归根结底还是要了解计算机体系,这样脱开编译器,不用 C 语言,你也能写出高性能代码。
PS:不要觉得丧心病狂,你们去看看 kernel 里各处性能相关的代码,看看 pypy 如何优化 python 的哈希表的,看看 jdk 的代码,这类优化比比皆是,其实写多了你也不会觉得难解。
--
常数范围裁剪
有时候你计算一个整数数值需要控制在 0 - 255 的范围,如果小于 0 那么等于零,如果大于 255,那么等于 255,做一个裁剪工作,可以用下面的位运算:
static inline int32_t clamp_to_0(int32_t x) { return ((-x) >> 31) & x;
}
static inline int32_t clamp_to_255(int32_t x) {return (((255 - x) >> 31) | x) & 255;
}
这个方法可以裁剪任何 2^n - 1 的常数,比如裁剪 65535:
static inline int32_t clamp_to_65535(int32_t x) {return (((65535 - x) >> 31) | x) & 65535;
}
略加改变即可实现,没有任何判断,没有任何分支。本技巧在不同架构下性能表现不一,具体看实测结果。
快速位扫描
假设你在设计一个容器,里面的容量需要按 2 次幂增加,这样对内存更友好些,即不管里面存了多少个东西,容量总是:2, 4, 8, 16, 32, 64 的刻度变化,假设容量是 x ,需要找到一个二次幂的新容量,刚好大于等于 x 怎么做呢?
static inline int next_size(int x) {int y = 1;while (y < x) y *= 2;return y;
}
一般会这样扫描一下,但是最坏情况上面循环需要迭代 31 次,如果是 64 位系统,类型是 size_t 的话,可能你需要迭代 63 次,假设你做个内存分配,分配器大小是二次幂增长的,那么每次分配都要一堆 for 循环来查找分配器大小的话,实在太坑爹了,于是继续位运算:
static inline uint32_t next_power_of_2(uint32_t x) {x--;x |= x >> 1; x |= x >> 2; x |= x >> 4; x |= x >> 8; x |= x >> 16; x++return x;
}
以及:
static inline uint32_t next_power_of_2(uint64_t x) {x--;x |= x >> 1; x |= x >> 2; x |= x >> 4; x |= x >> 8; x |= x >> 16; x |= x >> 32; x++return x;
}
在不用 gcc 内置 __builtin_clz 函数或 bsr 指令的情况下,这是 C 语言最 portable 的方案。
原文链接:https://www.zhihu.com/question/27417946/answer/1253126563?utm_campaign=shareopn&utm_medium=social&utm_psn=1783075953661992960&utm_source=wechat_session