能量不等式
这一部分需要知道的是能量的表达式
\[E(t)=\int_{0}^{l}u_{t}^{2}+a^{2}u_{x}^{2} dx
\]
一般而言题目常见的问法是证明能量是减少的，也就是我们需要证明
\[\dfrac{d}{dt}E(t) \le0
\]
在计算\(\dfrac{d}{dt}E(t) \le0\)的时候一定会用的题目给的方程条件去凑微分，还会用到Cauchy-Schwarz不等式放缩。
还要知道均方模的概念，例如\(u\)的均方模指的就是
\[E_{0}(t)=\int_{0}^{l}u^{2}dx
\]
在证明稳定性的时候我们会用到均方模。
以上是课本内容。标黄色部分是需要掌握的技巧。
例题 （课后题T1）
套路就是写出能量\(E(t)\)的表达式然后求导证明其单调不增，稳定性的证明就是去估计\(u(x,t)\)的均方模.
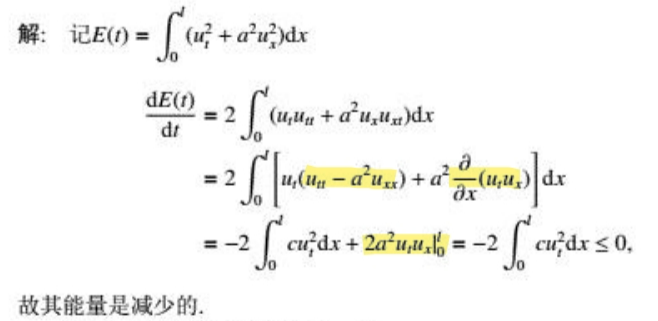
评注：在求导的时候，注意黄色标注的地方，一般会凑题目给定的方程（例如本题就是凑\(u_{tt}-a^{2}u_{xx}=cu_{t}\))，后面会正好凑成一个微分，这部分需要自己动笔算体会一下。
下面证明唯一性的问题
评注：唯一性就是假设有两个解\(u_{1}, u_{2}\)都满足方程, 去考虑\(u=u_{1}-u_{2}\), 由于叠加原理，这时候\(u\)满足的就是上图的齐次方程，再利用第一步得到的能量不等式，就可以得到\(u=0\), 就说明了唯一性。
下面证明稳定性，需要考虑均方模了，就是说初始条件的均方模很小的时候，解的均方模也很小，这就是稳定的含义。
\[E_{0}(t)=\int_{0}^{l}u^{2}dx
\]
\[\dfrac{d}{dt} E_{0}(t)=2\int_{0}^{l}uu_{t}dx\stackrel{\text{Cauchy-Schwarz}}{\leq} \int_{0}^{l}u^{2}dx+\int_{0}^{l}u_{t}^{2}dx=E_{0}(t)+E(t)
\]
式子两边同时乘\(e^{-t}\), 凑微分，得到
\[\dfrac{d}{dx}(E_{0}(t)e^{-t}) \le E(t)e^{-t}
\]
对上式从0到\(t\)积分，得到
\[E_{0}(t)e^{-t}-E_{0}(0)\le \int_{0}^{t} E(\tau)e^{-\tau} d\tau
\]
\[E_{0}(t)\le e^{t}\int_{0}^{t} E(\tau)e^{-\tau} d\tau +E_{0}(0)e^{t} \stackrel{\text{E(t)单调递减}}{\leq} E(0)(e^{t}-1)+E_{0}(0)e^{t}
\]
这就表明，初值\(E(0), E_{0}(0)\)很小的时候，解的均方模也很小。
评注：注意，我们刚刚是假设没有外力\(f\)作用下的均方模估计，所以只考虑了初值\(E(0), E_{0}(0)\)，如果有外力\(f\)，我们还需要利用\(f\)的均方模去说明稳定性，这就需要进一步的估计。
至此我们就完成了全部的证明。
评注：本题用到的技巧，无一例外都是来源于课本。
