相关概念
图 (graph) 是一个二元组 \(G=(V(G),E(G))\)。其中 \(V(G)\) 是非空集,称为 点集 (vertex set),对于 \(V\) 中的每个元素,我们称其为 顶点 (vertex) 或 节点 (node),简称 点;\(E(G)\) 为 \(V(G)\) 结点之间边的集合,称为 边集 (edge set)。
—— OI-Wiki
与树类似,同样使用结点和边来组织一张图,图上的一条边表示两个结点之间有关联。
但与树不同的是,图虽然也由顶点和边构成,但是它没有父亲和儿子的关系,任意两点之间的路径也可能并不唯一。
图可大致分为两种图, 无向图 (undirected graph) 和 有向图 (directed graph),混合图 (mixed graph) 可分为有部分双向边的有向图。
无向图中,如果有一条边连接 \(u\) 和 \(v\),则 \(u\) 可到 \(v\),\(v\) 也可到 \(u\)。
有向图中,如果有一条边表示从 \(u\) 到 \(v\),则 \(u\) 可到 \(v\),但 \(v\) 不可到 \(u\)。
图的概念很多,这里只写了较为重要的概念,详细的概念可见 图论相关概念 - OI Wiki。
带权图
从一张图的边进行分类,边上有权值的图称为 带权图,没有则称为 无权图。
简单图
如果一张图的任意两点之间,只含有最多一条边,即 重边,同时,不存在连接自己到自己的边,即 自环,那么这种图就叫做简单图。如果一张图允许存在自环和重边,那么这张图就不是简单图。
稠密图与稀疏图
对于无向图,我们知道 \(n\) 个顶点的无向图最多只有 \(\frac{n(n-1)}{2}\) 条边,对于有向图,最多有 \(n(n-1)\) 条边。对于一张简单图,它的边数几乎达到 \(O(n^2)\) 的图称为稠密图,边数差不多为 \(O(n)\) 的图称为稀疏图。
度
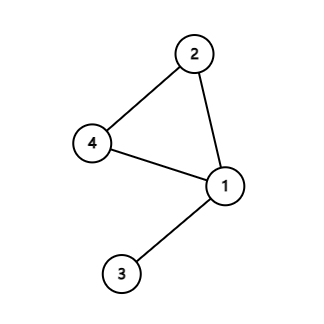
对于一张有向图中的一个结点 \(v\), 可直接到达 \(v\) 的结点数量称为 入度(in-degree),从 \(v\) 出发到达的结点数量称为 出度(out-degree)。如下图,\(1\) 的入度是 \(1\),出度是 \(2\),\(4\) 的入度是 \(2\),出度是 \(0\)。
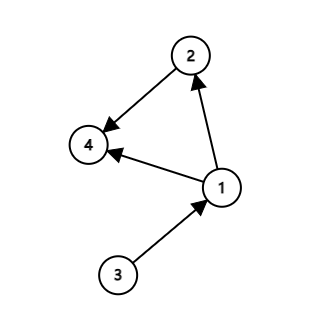
而对于一张无向图中的一个结点 \(v\),则只有 度(degree) 一说,结点 \(v\) 的 度(degree) 就是与顶点 \(v\) 相关联的结点的数量。如下图,\(1\) 的度是 \(3\),\(4\) 的度是 \(2\)。
连通
如果两个结点可通过一条路径互相到达,我们称之为这两个结点连通。
对于无向图,任意 两个结点都可以互相到达,那么我们叫这张图为连通图,反之则称为非连通图。
对于有向图,两个结点它们之间可以互相到达,我们称这两个结点为强连通,如果一个有向图上任意两个结点都可以互相到达,我们叫这张图为强连通图。
子图
我们取出一张图其中的一些顶点,以及保留两端都在这些顶点之中的边,这样构成的子图称为 顶点导出子图。
我们取出这张图的一些边,并保留这些边的顶点,这样构成的子图为边导出子图。
存储
邻接矩阵
邻接矩阵适用于稠密图,我们可以定义一个二维数组 \(g[][]\),对于 \(u\)、\(v\) 两个结点,我们可以用 \(g[u][v]\) 来表示这两个点有一条边,如果是带权图,则可以记录这条边的权值,构造的空间复杂度是 \(O(n^2)\),但查询两个结点的时间复杂度只有 \(O(1)\)。
\(\texttt{code}\)
int g[MAXN][MAXN];
......
for(int i=1;i<=m;i++){int u,v;cin>>u>>v;g[u][v]=1;//如果是无向图,这里应该是 g[u][v]=g[v][u]=1
}
邻接表
邻接表主要适用于稀疏图,我们定义 \(n\) 个向量,用于存储结点 \(u\) 可以直接到达的所有结点,如果是带权图,可以开一个结构体 node,含有二维信息 to 和 w,分别表示到达的顶点和这两个点之间的边权,当然也可以用 pair 来记录这两个值,空间复杂度 \(O(m)\),但是判断两个结点是否有连边,需要遍历整个 vector 查询,最坏时间复杂度 \(O(n)\)。
\(\texttt{code}\)
vector<int> g[MAXN];
......
for(int i=1;i<=m;i++){int u,v;cin>>u>>v;g[u].push_back(v);g[v].push_back(u);//无向图
}
//1struct node{int to,w;
}
vector<node> g[MAXN];
......
for(int i=1;i<=m;i++){int u,v,w;cin>>u>>v>>w;g[u].push_back((node){v,w});g[v].push_back((node){u,w});
}
//2vector<pair<int,int>> g[MAXN];
......
for(int i=1;i<=m;i++){int u,v,w;cin>>u>>v>>w;g[u].push_back(make_pair(v,w));g[v].push_back(make_pair(u,w));
}
//3
存边
除了以上两种存点的方式,还可以用结构体存储一条边,结构体中的成员变量 fr、to、w,分别表示这条边所连接的两个结点和这条边的边权,空间复杂度 \(O(m)\)。
struct Edge{int fr,to,w;
}edges[MAXN];
遍历
图的 bfs 遍历:
\(\texttt{code}\)
vector<int> g[MAXN];
void bfs(int s){queue<int> q;q.push(s);vis[s]=1;while(!q.empty()){int now=q.front();cout<<now<<" ";q.pop();for(auto x:g[now]){if(vis[x]==0){vis[x]=1;q.push(x);}}}
}
图的 dfs 遍历:
\(\texttt{code}\)
vector<int> g[MAXN];
void dfs(int now){cout<<now<<" ";vis[now]=1;for(auto x:g[now]){if(vis[x]==0){dfs(x);}}
}
以上两种写法的时间复杂度是 \(O(n+m)\)。
拓扑排序
对于一个有向无环图,有一个遍历顺序,是等一个结点的所有前驱结点都遍历完了,才遍历这个结点。这种顺序就叫做拓扑序。
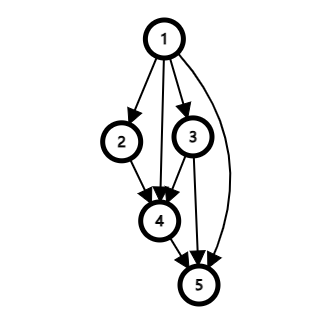
对于下面这张图,它的拓扑序可以是 1 2 3 4 5,而 1 2 4 3 5 则不是,因为 \(4\) 的前驱还有 \(3\) 没有遍历,必须先遍历 \(3\) 才能遍历 \(4\)。
int in[MAXN],res[MAXN];
vector<int> g[MAXN];
int num;
int topo(){for(int i=1;i<=n;i++){for(auto x:g[i]){in[x]++;}}queue<int> q;for(int i=1;i<=n;i++){if(in[i]==0){ q.push(i);}}while(!q.empty()){int k=q.front();q.pop();res[++num]=k;for(auto x:g[k]){in[x]--;if(in[x]==0){q.push(x);}}}if(num!=n){return false;}else{ return true;}
}
时间复杂度 \(O(n+m)\)。
欧拉路径问题
给你一个图,请你选择一个起点出发,经过所有的边,要求每条边只能经过一次,问能否达成目标,也称一笔画问题。
欧拉定理:如果一张连通图,只有 \(0\) 个或者 \(2\) 个结点,他的度为奇数,那么这张图可以一笔画。
证明:我们选择一个度数为奇数的顶点出发,走向一个度数为偶数的顶点,那么这个图变成了一个仍然满足上述性质但是结构更简单的图了。所以我们可以归纳证明上述定理。
对于这道题,我们可以使用 Hierholzer算法,它的思路是,对于欧拉回路,我相当于是将图拆成若干个环。所以我每次找图的正好一个环,如果没法找了,我就回溯地把这个环给存起来,存到栈中。
\(\texttt{code}\)
vector<pair<int,int>> g[MAXN];
stack<int> s;
int vis[maxm];//对边标记
void dfs(int now){for(auto x:g[now]){if(vis[x.second]==0){vis[x.second]=1;dfs(x.first);}}s.push(now);
}
时间复杂度 \(O(n+m)\)。
画图网站推荐