Codeforces Round 942 Div.2 题解

蹭个热度，挽救一下 cnblogs 蒸蒸日上的阅读量。

Q: 你是手速狗吗？

A: 我觉得我是。

2A

因为选的 \(w\) 一定可以让它合法，一次操作可以看作 \(a\) 数组向右平移一位。枚举操作次数后暴力判断即可。

#include <bits/stdc++.h>void work() {int n;std::cin >> n;std::vector<int> a(n + 1, 0), b(n + 1, 0);for (int i = 1; i <= n; ++i)std::cin >> a[i];for (int i = 1; i <= n; ++i)std::cin >> b[i];for (int x = 0; x <= n; ++x) {bool flg = true;for (int i = 1; i <= n - x; ++i)flg &= a[i] <= b[i + x];if (flg) return std::cout << x << '\n', void();}return;
}int main() {std::cin.tie(nullptr)->sync_with_stdio(false);int t; std::cin >> t;while (t--) work();return 0;
}

2B

将 U 视作 \(1\)，将 D 视作 \(0\)，一次操作就是拿走一个 \(1\)，将两侧分别异或 \(1\)。

观察一下样例，盲猜 U 有奇数个先手赢，反之后手赢。来理解一下。

根据上述转化，判定条件等价于判断全局异或和为 \(0\) 还是为 \(1\)。一次操作对全局异或和的影响是，将其异或上 \(1\)。

初始异或和为 \(1\) 时，先手 必定 可以操作，到后手时异或和为 \(0\)，后手 可能 可以操作，回到先手，异或和还是 \(1\)，必定 可以操作。如此往复，只要后手能操作，先手必定可以操作。

另一种情况类似。

感觉这个题挺有意思的，突破点在于对一次操作影响的观察。

#include <bits/stdc++.h>void work() {int n;std::cin >> n;std::string s;std::cin >> s;int cnt = 0;for (int i = 0; i < n; ++i)if (s[i] == 'U') ++cnt;if (!cnt) return std::cout << "NO\n", void();if (cnt & 1) {std::cout << "YES\n";} else {std::cout << "NO\n";}return;
}int main() {std::cin.tie(nullptr)->sync_with_stdio(false);int t; std::cin >> t;while (t--) work();return 0;
}

2C / 1A

顺着自己的感觉走，我们应该会想到尽量让 \(a\) “平均”，也就是 \(k\) 优先给小的分配。

画一画会发现最 “紧凑” 的结构是 \(1,2,3,4,1,2,3,4\) 这样的模式，直觉上很对，因为 “利用率” 最高。

将贡献写出来，假设最小值为 \(x\)，比 \(x\) 大的有 \(y\) 个，我们一定会把这 \(y\) 个尽量往前放，让较小的 \(x\) 利用充分，这样总共有 \((x-1)n+1+y\) 个合法子段。

然后就是模拟，把 \(k\) 尽量往小的分。差分维护即可。

时间复杂度 \(\mathcal O(n\log n)\)，瓶颈在排序。

#include <bits/stdc++.h>using i64 = long long;void work() {int n;i64 k;std::cin >> n >> k;std::vector<i64> a(n, 0);for (int i = 0; i < n; ++i)std::cin >> a[i];std::sort(a.begin(), a.end());std::vector<i64> dlt(n, 0);for (int i = 0; i < n - 1; ++i) {if (!k) break;i64 x = 1ll * (i + 1) * (a[i + 1] - a[i]);if (k >= x) {dlt[i] += a[i + 1] - a[i];k -= x;} else {i64 d = k / (i64)(i + 1);for (int j = 0; j <= i; ++j)a[j] += d;k -= 1ll * (i + 1) * d;for (int j = i; ~j; --j)if (k) ++a[j], --k;break;}}i64 sum = 0;for (int i = n - 1; ~i; --i)sum += dlt[i], a[i] += sum;i64 d = k / (i64)n;k -= 1ll * n * d;for (int i = n - 1; ~i; --i)a[i] += d;for (int i = n - 1; ~i; --i)if (k) ++a[i], --k;i64 res = 0;for (int i = n - 1; ~i; --i)if (a[i] > a[0]) ++res;std::cout << 1ll * a[0] * n - n + 1 + res << '\n';return;
}int main() {std::cin.tie(nullptr)->sync_with_stdio(false);int t; std::cin >> t;while (t--) work();return 0;
}

2D / 1B

• D1

枚举 \(d=\gcd(a,b)\)，令 \(a\gets a/d,b\gets b/d\)，我们要求 \(\gcd(a,b)=1,bd|(a+b)\)。

要满足这个限制，必然有 \(a=(kd-1)b\)，又因为 \(\gcd(a,b)=1\)，所以 \(b=1\)。

于是枚举 \(d,a\)，判断是否有 \(d|(a+1)\) 即可。根据调和级数的经典结论，时间复杂度 \(\mathcal O(\sum n\ln n)\)。可以更快但场上写这个方便。

#include <bits/stdc++.h>using i64 = long long;void work() {int n, m;std::cin >> n >> m;i64 ans = 0;for (int d = 1; d <= n && d <= m; ++d) {for (int a = 1; a * d <= n; ++a)if ((a + 1) % d == 0) ++ans;}std::cout << ans << '\n';return;
}int main() {std::cin.tie(nullptr)->sync_with_stdio(false);int t; std::cin >> t;while (t--) work();return 0;
}

• D2

前排提示：非正解。

按照剧本，继续枚举 \(d=\gcd(a,b),a\gets a/d,b\gets b/d\)，要有 \((a+b)|bd\)。

因为此时 \(\gcd(a,b)=1\)，所以 \((a+b)\not| \ b\)，于是 \((a+b)|d\)。

枚举 \(d\) 的因子 \(x\)，再枚举 \(b\)，令 \(a=x-b\)，判一下是否有 \(\gcd(a,b)=1\) 且 \(a,b\) 都满足边界限制即可。

场上我只是打了个这个代码来检验正确性，测了一下样例发现跑得飞快，\(n,m\) 取满也只有 1e7 左右个合法数对，0.5s 就能跑出来，交上去直接 pp 了，也没 fst。

正解好像挺智慧，不太会。

#include <bits/stdc++.h>using i64 = long long;int gcd(int x, int y) { return y ? gcd(y, x % y) : x; }void work() {int n, m;std::cin >> n >> m;int ans = 0;for (int d = 1; d <= n && d <= m; ++d) {int lmt = (n / d) + (m / d);for (int x = 2; x <= d && x <= lmt; ++x) {if (d % x) continue ;for (int b = 1; b < x && b * d <= m; ++b) {int a = x - b;if (a >= 1 && a * d <= n && gcd(a, b) == 1)++ans;}}}std::cout << ans << '\n';return;
}int main() {std::cin.tie(nullptr)->sync_with_stdio(false);int t; std::cin >> t;while (t--) work();return 0;
}

2E / 1C

有一种 CNOI 模拟赛的美。

首先发现增量构造非常对，因为 \(a_i\) 对 \(i\) 这个节点的贡献无论多少轮都是 \(a_i\)，于是只要确定了 \(a_{1\sim i-1}\) 就可以直接知道 \(a_i\) 是啥。

此时我们需要知道 \(a_{1\sim i-1}\) 做了 \(k\) 轮后对 \(i\) 的贡献，显然对于 \(j\in [1,i-1]\)，\(a_j\) 的贡献系数是独立的。

假设树状数组上 \(j\) 到 \(i\) 有 \(n\) 个点，做 \(k\) 轮这个过程的贡献系数是 \(\dbinom{n+k-2}{k-1}\)。

这个系数咋看出来？我不太会直接推导，只能讲讲咋找规律。手摸几次操作应该会看出来和二项式系数有关系，每行前面 1, 2 较简单的可以直接写成二项式系数，其余项根据 \(s_i=s_{i-1}+a_i\) 的公式，联想一下递推公式 \(\dbinom{n}{m}=\dbinom{n-1}{m-1}+\dbinom{n-1}{m}\) 凑一下就行。

正常的方法是组合推导，或者拉格朗日插值。

回到正文，得到贡献系数以后，根据吸收恒等式 \(\dbinom{n}{m}=\dfrac nm \dbinom{n-1}{m-1}\) 在树状数组上计算即可。\(\mathcal O(n\log n)\)。

#include <bits/stdc++.h>
#define pb emplace_back
#define fir first
#define sec secondusing i64 = long long;
using pii = std::pair<int, int>;constexpr int mod = 998244353;
constexpr int maxn = 2e5 + 5;
void Add(int& x, int y) { if ((x += y) >= mod) x -= mod; return ; }
void sub(int& x, int y) { if ((x -= y) < 0) x += mod; return ; }
int n, k, a[maxn], inv[maxn];struct Fenwick {int c[maxn];Fenwick() { memset(c, 0, sizeof(c)); }void clr(int n) { std::fill(c, c + 1 + n, 0); return; }void add(int x, int y) {int coef = 1, cnt = 1;for (; x <= n; x += x & -x) {Add(c[x], 1ll * y * coef % mod);++cnt;coef = 1ll * coef * (cnt + k - 2) % mod * inv[cnt - 1] % mod;}return;} 
} tr;void init(int n) {inv[1] = 1;for (int i = 2; i <= n; ++i)inv[i] = 1ll * (mod - mod / i) * inv[mod % i] % mod;return;
}void work() {std::cin >> n >> k;for (int i = 1; i <= n; ++i)std::cin >> a[i];tr.clr(n);for (int i = 1; i <= n; ++i) {int x = a[i];sub(x, tr.c[i]);tr.add(i, x);std::cout << x << ' ';}std::cout << '\n';return;
}int main() {init(maxn - 1);std::cin.tie(nullptr)->sync_with_stdio(false);int t;std::cin >> t;while (t--) work();return 0;
}

2F / 1D

被爆了 /kk。

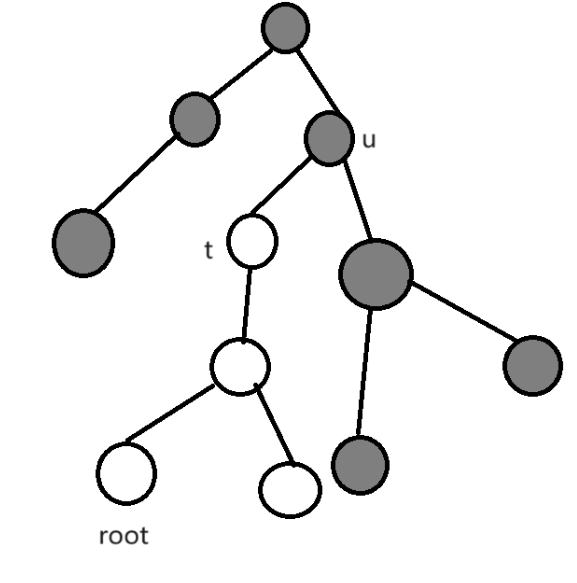
直接做是很困难的，考虑二分答案 \(mid\)，每个位置的操作都是独立的，连边 \(i\to b_i\) 得到一个基环树森林，\(a_i\) 能变成的数就是 \(a_i\) 在基环树上走 \(\le mid\) 步能到达的点。

此时有一个显然的贪心：对于 \(i\)，选一个 \(\ge a_{i-1}\) 的，\(a_i\) 能到达的最小的 \(x\)，\(a_i\gets x\)。

涉及树链上点权前驱，主席树优化一下可以 log^2，但是 N_z 表示专门卡掉了这个算法。

转换视角：我们不再让 \(a_i\) 去找他能到达的点的前驱，而是去尝试将一个数填入 \(a_i\)。其实是一个 two-pointers 的 trick。

具体地，令 \(j=1\)，顺序遍历，假设当前遍历到 \(a_i\)，如果 \(a_i\) 能通过 \(\le mid\) 步到达 \(j\)，则 \(a_i\gets j\)，反之 \(j\gets j+1\)，如果 \(j>m\) 则无解。

判断 \(a_i\) 是否能通过 \(\le mid\) 步到达 \(j\) 是简单的，时间复杂度 \(\mathcal O((n+m)\log m)\)，有点 dirty work，不想碰基环树。

luanmenglei 大神说的很有道理：这题的难点在于你不把它当成一个大 DS 题。

#include <bits/stdc++.h>
#define pb emplace_back
#define fir first
#define sec secondusing i64 = long long;
using pii = std::pair<int, int>;constexpr int maxn = 1e6 + 5;
int n, m, r, rt[maxn], a[maxn], b[maxn], dfc, dfn[maxn], siz[maxn], bel[maxn], cnt, onc[maxn], dep[maxn], sic[maxn];
bool vis[maxn];
std::vector<int> G[maxn];void dfs(int u, int ff) {dep[u] = dep[ff] + 1;dfn[u] = ++dfc;siz[u] = 1;rt[u] = r;for (auto& v : G[u]) {if (onc[v] || dfn[v] || v == ff) continue ;dfs(v, u);siz[u] += siz[v];}return;
}bool check(int L) {auto cov = [&](int x, int y) {return dfn[x] <= dfn[y] && dfn[y] < dfn[x] + siz[x];};auto myabs = [&](int x) {return x > 0 ? x : -x;};auto chk = [&](int x, int y) {if (bel[x] != bel[y]) return false;if (onc[x] && onc[y]) {int d = (sic[bel[x]] + onc[x] - onc[y]) % sic[bel[x]];return d <= L;} else if (onc[y]) {int d = dep[x] - 1;x = rt[x];d += (sic[bel[x]] + onc[x] - onc[y]) % sic[bel[x]];return d <= L;} else if (onc[x]) {return false;} else {return cov(y, x) && dep[x] - dep[y] <= L;}return true;};for (int i = 1, j = 1; i <= n; ++i) {for (; j <= m; ++j) if (chk(a[i], j)) break;if (j > m) return false;}return true;
}void work() {std::cin >> n >> m;for (int i = 1; i <= n; ++i)std::cin >> a[i];for (int i = 1; i <= m; ++i)G[i].clear();for (int i = 1; i <= m; ++i) {std::cin >> b[i];G[b[i]].pb(i);}std::fill(vis + 1, vis + 1 + m, false);std::fill(onc + 1, onc + 1 + m, 0);std::fill(dep + 1, dep + 1 + m, 0);std::fill(bel + 1, bel + 1 + m, 0);std::fill(sic + 1, sic + 1 + m, 0);for (int i = 1; i <= m; ++i) {if (vis[i]) continue ;std::vector<int> pth;for (int x = i; !vis[x]; x = b[x])pth.pb(x), vis[x] = true;int x = pth.back();if (bel[b[x]]) {for (auto& v : pth)bel[v] = bel[b[x]];continue; }std::vector<int> cyc;x = b[x];while (pth.back() != x) cyc.pb(pth.back()), pth.pop_back();pth.pop_back();cyc.pb(x);std::reverse(pth.begin(), pth.end());++cnt;sic[cnt] = cyc.size();for (int i = 0; i < cyc.size(); ++i)onc[cyc[i]] = i + 1, bel[cyc[i]] = cnt;for (auto& v : pth)bel[v] = cnt;}std::fill(siz + 1, siz + 1 + m, 0);std::fill(dfn + 1, dfn + 1 + m, 0);std::fill(rt + 1, rt + 1 + m, 0);for (int i = 1; i <= m; ++i)assert(bel[i] > 0);dfc = 0;for (int i = 1; i <= m; ++i)if (onc[i]) r = i, dfs(i, 0);int l = 0, r = m;while (l <= r) {int mid = (l + r) >> 1;if (check(mid)) {r = mid - 1;} else {l = mid + 1;}}std::cout << (check(l) ? l : -1) << '\n';return;
}int main() {std::cin.tie(nullptr)->sync_with_stdio(false);int t; std::cin >> t;while (t--) work();return 0;
}

1E

不会格路计数，不会反射容斥 /chandou。